11xy^{-1}z^{0} / v^{-3}
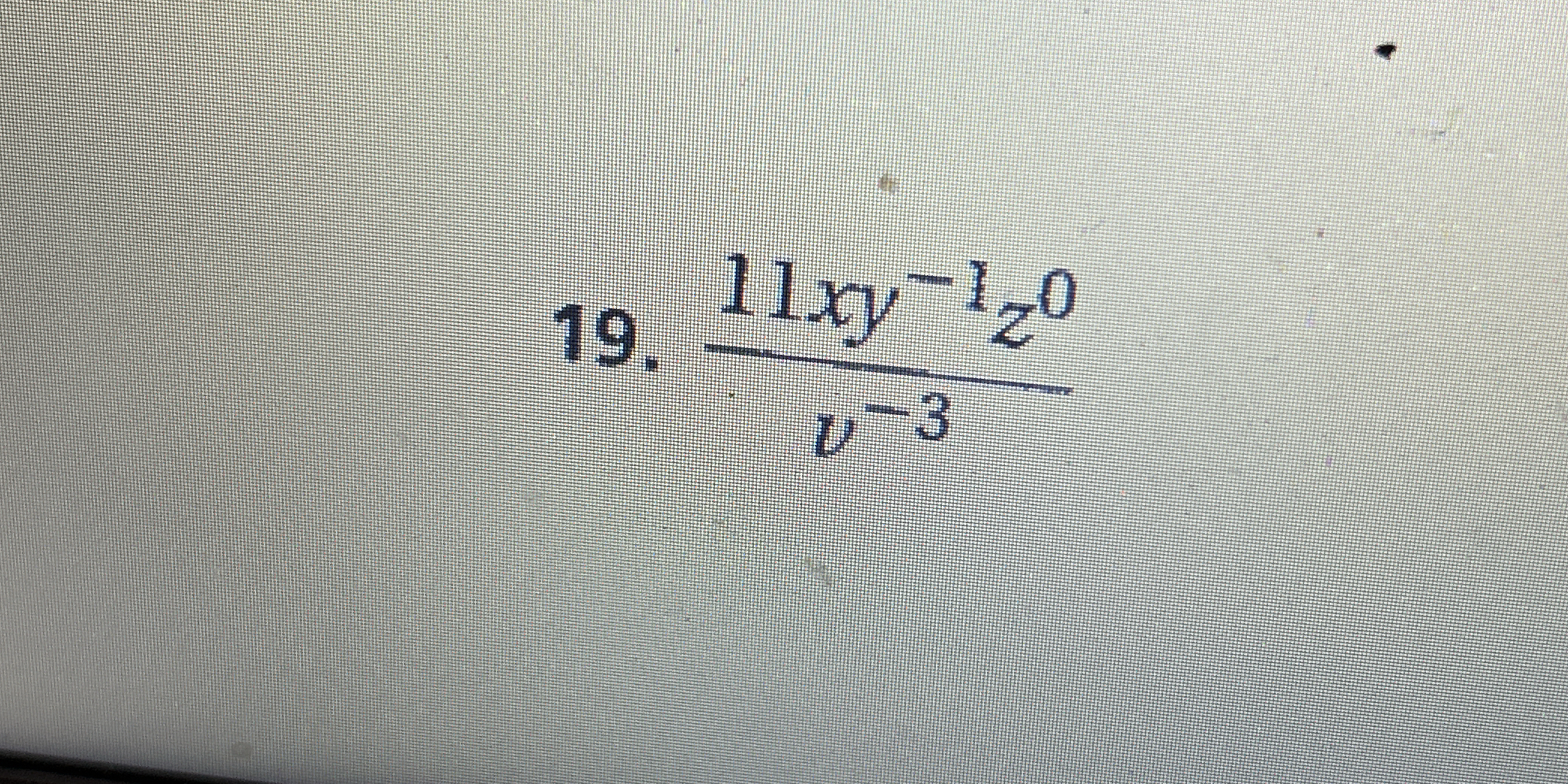
Understand the Problem
The question presents a mathematical expression that includes variables and may require simplification or evaluation. We will identify the expression and analyze its components.
Answer
The simplified expression is $$ \frac{11xv^3}{y} $$
Answer for screen readers
The simplified expression is
$$ \frac{11xv^3}{y} $$
Steps to Solve
- Identify and simplify the expression components
The expression is given by
$$ \frac{11xy^{-1}z^{0}}{v^{-3}} $$
Here, we can simplify:
- The term $z^{0}$ is equal to $1$ (since any number raised to the power of 0 is 1).
- The term $y^{-1}$ can be rewritten as $\frac{1}{y}$.
- The term $v^{-3}$ can be rewritten as $\frac{1}{v^3}$ in the denominator, which means it will be moved to the numerator as $v^3$.
So the expression simplifies to:
$$ \frac{11x \cdot \frac{1}{y} \cdot 1}{\frac{1}{v^3}} = 11x \cdot \frac{1}{y} \cdot v^3 $$
- Reorganize the simplified expression
We need to organize our final expression in a standard multi-variable format.
Thus we have:
$$ \frac{11x v^3}{y} $$
- Final expression interpretation
The final expression after complete simplification is:
$$ \frac{11xv^3}{y} $$
This shows the relationship between the variables clearly, incorporating all the necessary components.
The simplified expression is
$$ \frac{11xv^3}{y} $$
More Information
The simplification of expressions like these is common in algebra, especially when dealing with negative and zero exponents. Understanding how to manipulate exponents helps in various applications in mathematics and sciences.
Tips
- Forgetting that $z^0 = 1$ is a common oversight; always remember to simplify expressions with zero exponents.
- Confusing $y^{-1}$ with $y$; it's important to remember that it transforms into $\frac{1}{y}$.
- Not properly dealing with negative exponents in the denominator can lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information