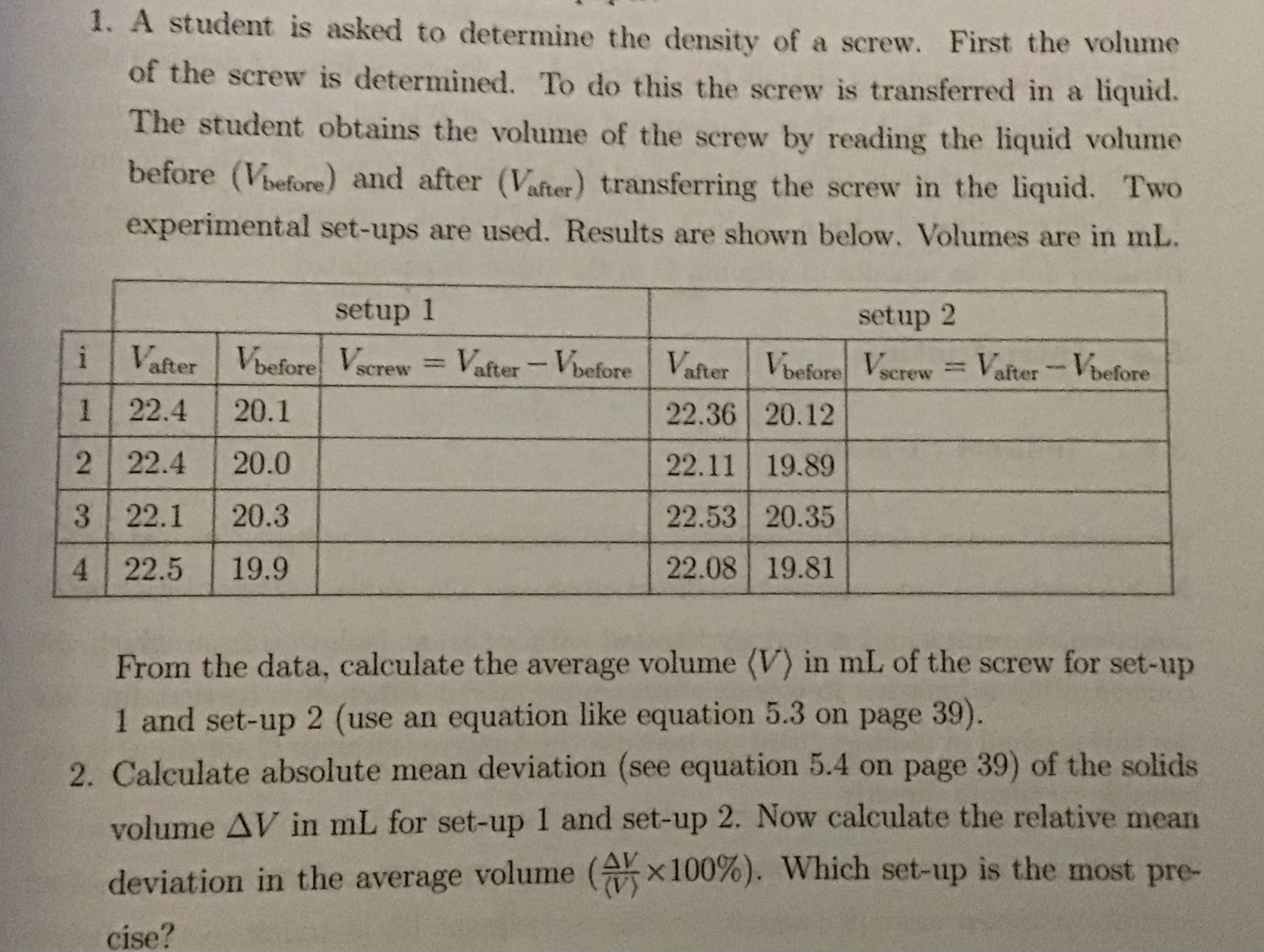
1. From the data, calculate the average volume (V) in mL of the screw for setup 1 and setup 2 (use an equation like equation 5.3 on page 39). 2. Calculate absolute mean deviation (... 1. From the data, calculate the average volume (V) in mL of the screw for setup 1 and setup 2 (use an equation like equation 5.3 on page 39). 2. Calculate absolute mean deviation (see equation 5.4 on page 39) of the solids volume ΔV in mL for setup 1 and setup 2. Now calculate the relative mean deviation in the average volume ($\frac{\Delta V}{\langle V \rangle} \times 100\%$). Which setup is the most precise?
Understand the Problem
This is a problem about calculating the average volume of a screw using two different experimental setups, as well as finding the absolute and relative mean deviations to determine which setup is more precise. We need to use the provided data and the formulas mentioned (equations 5.3 and 5.4) to perform these calculations.
Answer
1. $\langle V \rangle_{setup \, 1} = 2.275 \, \text{mL}$, $\langle V \rangle_{setup \, 2} = 2.2275 \, \text{mL}$ 2. $\Delta V_{setup \, 1} = 0.2375 \, \text{mL}$, $\Delta V_{setup \, 2} = 0.0275 \, \text{mL}$, Relative deviation$_{setup \, 1}= 10.44\%$, Relative deviation$_{setup \, 2} = 1.234\%$. Set-up 2 is more precise.
Answer for screen readers
- Average volume for set-up 1: $\langle V \rangle = 2.275 , \text{mL}$ Average volume for set-up 2: $\langle V \rangle = 2.2275 , \text{mL}$
- Absolute mean deviation for set-up 1: $\Delta V = 0.2375 , \text{mL}$ Absolute mean deviation for set-up 2: $\Delta V = 0.0275 , \text{mL}$ Relative mean deviation for set-up 1: $10.44%$ Relative mean deviation for set-up 2: $1.234%$ Set-up 2 is the most precise.
Steps to Solve
- Calculate $V_{screw}$ for each trial in setup 1
$V_{screw} = V_{after} - V_{before}$
Trial 1: $V_{screw} = 22.4 - 20.1 = 2.3 , \text{mL}$
Trial 2: $V_{screw} = 22.4 - 20.0 = 2.4 , \text{mL}$
Trial 3: $V_{screw} = 22.1 - 20.3 = 1.8 , \text{mL}$
Trial 4: $V_{screw} = 22.5 - 19.9 = 2.6 , \text{mL}$
- Calculate $V_{screw}$ for each trial in setup 2
$V_{screw} = V_{after} - V_{before}$
Trial 1: $V_{screw} = 22.36 - 20.12 = 2.24 , \text{mL}$
Trial 2: $V_{screw} = 22.11 - 19.89 = 2.22 , \text{mL}$
Trial 3: $V_{screw} = 22.53 - 20.35 = 2.18 , \text{mL}$
Trial 4: $V_{screw} = 22.08 - 19.81 = 2.27 , \text{mL}$
- Calculate the average volume $\langle V \rangle$ for setup 1
$\langle V \rangle = \frac{\sum V_{screw}}{n} = \frac{2.3 + 2.4 + 1.8 + 2.6}{4} = \frac{9.1}{4} = 2.275 , \text{mL}$
- Calculate the average volume $\langle V \rangle$ for setup 2
$\langle V \rangle = \frac{\sum V_{screw}}{n} = \frac{2.24 + 2.22 + 2.18 + 2.27}{4} = \frac{8.91}{4} = 2.2275 , \text{mL}$
- Calculate the absolute mean deviation $\Delta V$ for setup 1
$\Delta V = \frac{\sum |V_{screw} - \langle V \rangle|}{n}$
$\Delta V = \frac{|2.3 - 2.275| + |2.4 - 2.275| + |1.8 - 2.275| + |2.6 - 2.275|}{4}$
$\Delta V = \frac{0.025 + 0.125 + 0.475 + 0.325}{4} = \frac{0.95}{4} = 0.2375 , \text{mL}$
- Calculate the absolute mean deviation $\Delta V$ for setup 2
$\Delta V = \frac{\sum |V_{screw} - \langle V \rangle|}{n}$
$\Delta V = \frac{|2.24 - 2.2275| + |2.22 - 2.2275| + |2.18 - 2.2275| + |2.27 - 2.2275|}{4}$
$\Delta V = \frac{0.0125 + 0.0075 + 0.0475 + 0.0425}{4} = \frac{0.11}{4} = 0.0275 , \text{mL}$
- Calculate the relative mean deviation for setup 1
$\frac{\Delta V}{\langle V \rangle} \times 100% = \frac{0.2375}{2.275} \times 100% = 0.1044 \times 100% = 10.44%$
- Calculate the relative mean deviation for setup 2
$\frac{\Delta V}{\langle V \rangle} \times 100% = \frac{0.0275}{2.2275} \times 100% = 0.01234 \times 100% = 1.234%$
- Determine which setup is more precise
Since setup 2 has a lower relative mean deviation (1.234%) compared to setup 1 (10.44%), setup 2 is more precise.
- Average volume for set-up 1: $\langle V \rangle = 2.275 , \text{mL}$ Average volume for set-up 2: $\langle V \rangle = 2.2275 , \text{mL}$
- Absolute mean deviation for set-up 1: $\Delta V = 0.2375 , \text{mL}$ Absolute mean deviation for set-up 2: $\Delta V = 0.0275 , \text{mL}$ Relative mean deviation for set-up 1: $10.44%$ Relative mean deviation for set-up 2: $1.234%$ Set-up 2 is the most precise.
More Information
Precision refers to the repeatability or reproducibility of a measurement. A more precise measurement will have a smaller deviation from the mean. In this case, setup 2 is more precise because it has a lower relative mean deviation which indicates that individual measurements are closer to the average volume.
Tips
- Forgetting to take the absolute value when calculating the absolute mean deviation.
- Using the wrong formula for calculating average volume or absolute mean deviation.
- Making arithmetic errors during calculations (addition, subtraction, division).
- Incorrectly identifying which setup is more precise based on the relative mean deviation.
AI-generated content may contain errors. Please verify critical information