1. Determine the average rate of change. 2. Find an equation for the line that is tangent to the graph of the function at x = 1. 3. Calculate the slope of the tangent to the given... 1. Determine the average rate of change. 2. Find an equation for the line that is tangent to the graph of the function at x = 1. 3. Calculate the slope of the tangent to the given function at the given point value of x. a. f(x) = 3/(x+1), P(2, 1) b. g(x) = sqrt(x + 2), P(-1, 1) c. h(x) = 2/sqrt(x+5), P(4, 2/3) d. f(x) = 5/(x-2), P(4, 5/2) 4. Calculate the slope of the graph of f(x) = {4 - x^2, if x <= 1; 2x + 1, if x > 1} at each of the following points: a. P(-1,3) b. P(2,5) 5. The height, in metres, of an object that has fallen from a height of 180
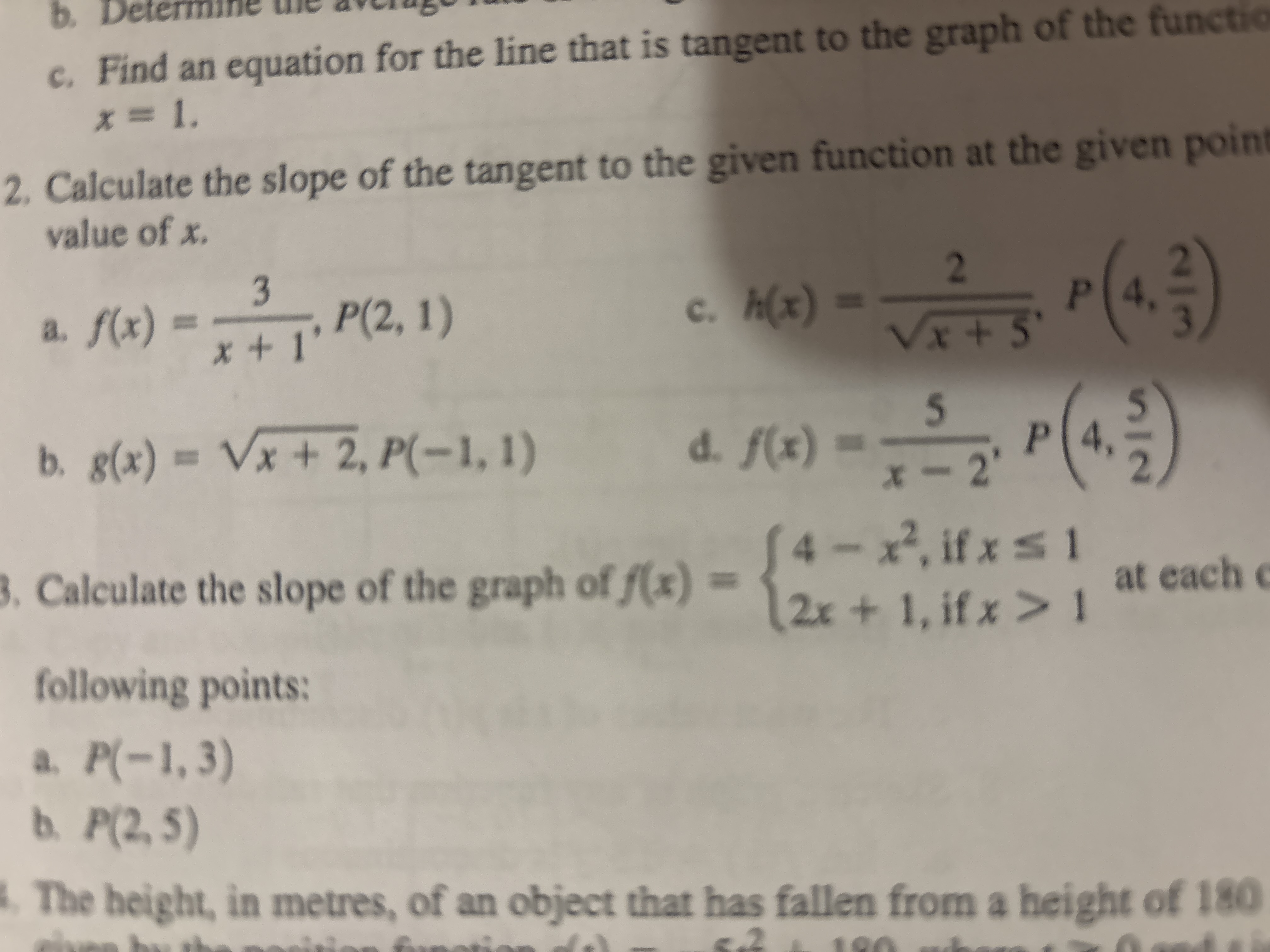
Understand the Problem
The image presents a set of calculus problems typically found in a homework assignment. The problems involve finding equations of tangent lines, calculating slopes of tangent lines at given points, and working with piecewise-defined functions. We need to use differentiation to find the slopes and tangent lines.
Answer
2a. $-\frac{1}{3}$ 2b. $\frac{1}{2}$ 2c. $-\frac{1}{98}$ 2d. $-\frac{5}{4}$ 3a. $2$ 3b. $2$
Answer for screen readers
2a. $ -\frac{1}{3} $ 2b. $ \frac{1}{2} $ 2c. $ -\frac{1}{98} $ 2d. $ -\frac{5}{4} $ 3a. $ 2 $ 3b. $ 2 $
Steps to Solve
- Problem 2a: Find the derivative of $f(x) = \frac{3}{x+1}$
To find the slope of the tangent line, we need to find the derivative of the function $f(x)$. We can rewrite the function as $f(x) = 3(x+1)^{-1}$. Using the power rule and chain rule, we have: $f'(x) = -3(x+1)^{-2} = \frac{-3}{(x+1)^2}$
- Problem 2a: Evaluate the derivative at $x=2$
Now, we need to evaluate the derivative at $x=2$ to find the slope of the tangent at the point $P(2,1)$: $f'(2) = \frac{-3}{(2+1)^2} = \frac{-3}{3^2} = \frac{-3}{9} = -\frac{1}{3}$
- Problem 2b: Find the derivative of $g(x) = \sqrt{x+2}$
We can rewrite the function as $g(x) = (x+2)^{\frac{1}{2}}$. Using the power rule and chain rule, we have: $g'(x) = \frac{1}{2}(x+2)^{-\frac{1}{2}} = \frac{1}{2\sqrt{x+2}}$
- Problem 2b: Evaluate the derivative at $x=-1$
Now, we need to evaluate the derivative at $x=-1$ to find the slope of the tangent at the point $P(-1,1)$: $g'(-1) = \frac{1}{2\sqrt{-1+2}} = \frac{1}{2\sqrt{1}} = \frac{1}{2}$
- Problem 2c: Find the derivative of $h(x) = \frac{2}{\sqrt{x}+5}$
Rewrite the function as $h(x) = \frac{2}{x^{1/2} + 5}$. Then, the derivative is: $h'(x) = \frac{-2(\frac{1}{2}x^{-1/2})}{(x^{1/2} + 5)^2} = \frac{-x^{-1/2}}{(x^{1/2} + 5)^2} = \frac{-1}{\sqrt{x}(\sqrt{x}+5)^2}$
- Problem 2c: Evaluate the derivative at $x=4$
Now, we need to evaluate the derivative at $x=4$: $h'(4) = \frac{-1}{\sqrt{4}(\sqrt{4}+5)^2} = \frac{-1}{2(2+5)^2} = \frac{-1}{2(7)^2} = \frac{-1}{2(49)} = -\frac{1}{98}$
- Problem 2d: Find the derivative of $f(x) = \frac{5}{x-2}$
Rewrite the function as $f(x) = 5(x-2)^{-1}$. Using the power rule and chain rule, we have: $f'(x) = -5(x-2)^{-2} = \frac{-5}{(x-2)^2}$
- Problem 2d: Evaluate the derivative at $x=4$
Now, we need to evaluate the derivative at $x=4$: $f'(4) = \frac{-5}{(4-2)^2} = \frac{-5}{2^2} = \frac{-5}{4}$
- Problem 3a: Find the slope of $f(x)$ at $P(-1,3)$
$f(x) = \begin{cases} 4-x^2, & \text{if } x \leq 1 \ 2x+1, & \text{if } x > 1 \end{cases}$
Since $x = -1 \le 1$, we use $f(x) = 4 - x^2$.
$f'(x) = -2x$ $f'(-1) = -2(-1) = 2$
- Problem 3b: Find the slope of $f(x)$ at $P(2,5)$
Since $x=2 > 1$, we use $f(x) = 2x+1$.
$f'(x) = 2$ $f'(2) = 2$
2a. $ -\frac{1}{3} $ 2b. $ \frac{1}{2} $ 2c. $ -\frac{1}{98} $ 2d. $ -\frac{5}{4} $ 3a. $ 2 $ 3b. $ 2 $
More Information
These solutions involve finding derivatives of various functions and then evaluating those derivatives at specific points to find the slope of the tangent line at those points. For piecewise functions, it is important to use the correct piece of the function based on the $x$ value.
Tips
- Forgetting the chain rule when taking derivatives.
- Making mistakes with negative signs.
- Using the wrong piece of the piecewise function.
- Incorrectly applying the power rule or quotient rule.
- Simplifying derivatives incorrectly.
- Not evaluating the derivative at the correct x-value.
AI-generated content may contain errors. Please verify critical information