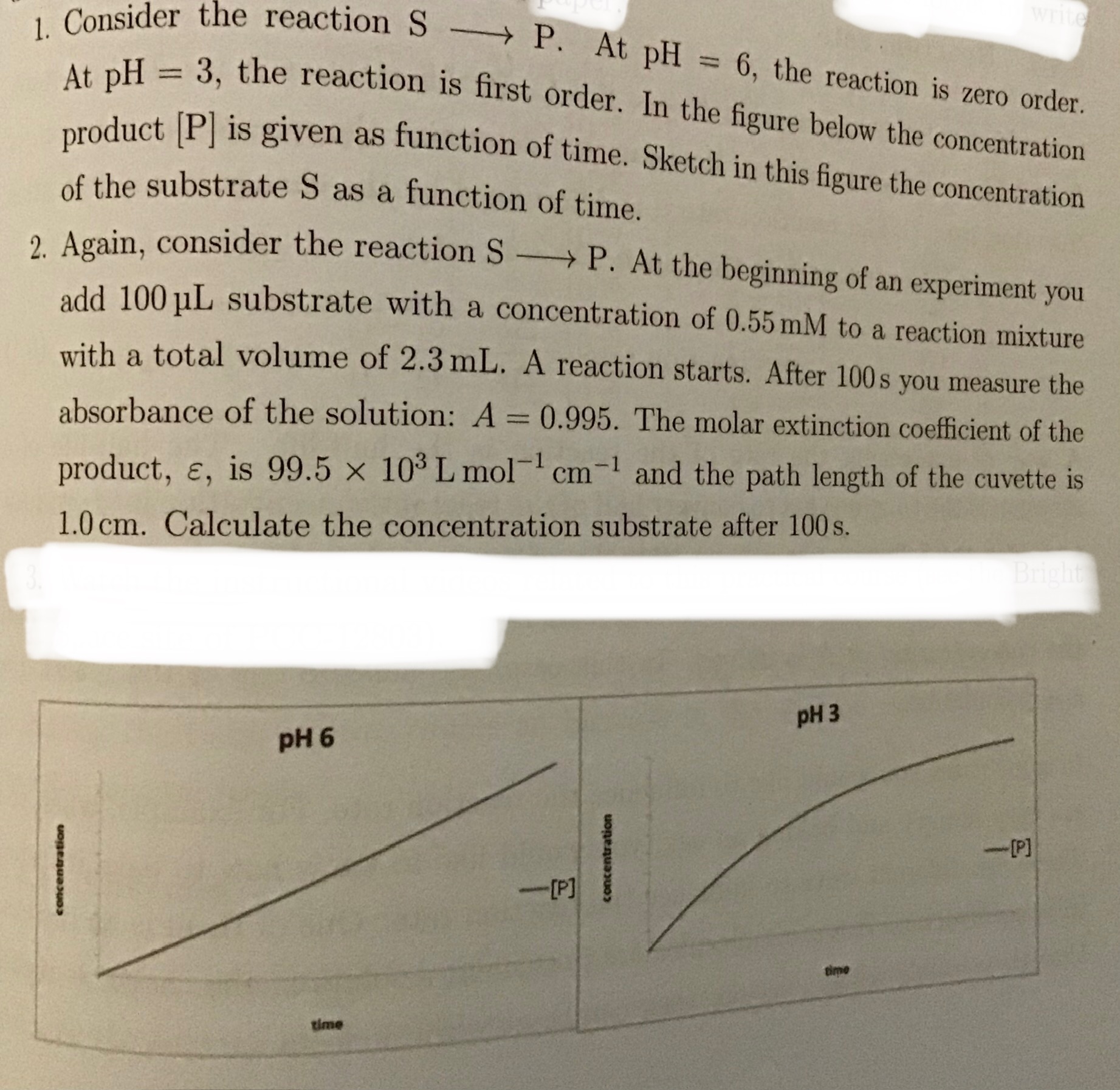
1. Consider the reaction S -> P. At pH = 3, the reaction is first order. At pH = 6, the reaction is zero order. In the figure below the concentration product [P] is given as functi... 1. Consider the reaction S -> P. At pH = 3, the reaction is first order. At pH = 6, the reaction is zero order. In the figure below the concentration product [P] is given as function of time. Sketch in this figure the concentration of the substrate S as a function of time. 2. Again, consider the reaction S -> P. At the beginning of an experiment you add 100 µL substrate with a concentration of 0.55 mM to a reaction mixture with a total volume of 2.3 mL. A reaction starts. After 100s you measure the absorbance of the solution: A = 0.995. The molar extinction coefficient of the product, ε, is 99.5 × 10^3 L mol^-1 cm^-1 and the path length of the cuvette is 1.0 cm. Calculate the concentration substrate after 100 s. Read more

Steps to Solve

1. Sketching the concentration of S at pH = 6

Since the reaction is zero order at pH = 6, the rate of the reaction is independent of the substrate concentration i.e. the substrate S decreases linearly with time, and the plot of [S] vs time will be a straight line with a negative slope.

2. Sketching the concentration of S at pH = 3

Since the reaction is first order at pH = 3, the rate of the reaction is proportional to the substrate concentration. Thus the substrate S decreases exponentially with time and the plot of [S] vs time will show a decay that starts rapidly and slows down as the reaction progresses.

3. Calculating the initial concentration of substrate

The initial concentration of the added substrate must be calculated taking into account the dilution. $C_1V_1 = C_2V_2$ where $C_1$ is the initial concentration of the substrate, $V_1$ is the initial volume of the substrate, $C_2$ is the final concentration of the substrate, and $V_2$ is the final volume of the solution. $$ (0.55 \text{ mM})(100 \text{ } \mu \text{L}) = C_2(2.3 \text{ mL}) $$ First we must convert $100 \text{ } \mu \text{L}$ to mL $100 \text{ } \mu \text{L} = 0.1 \text{ mL}$ $$ (0.55 \text{ mM})(0.1 \text{ mL}) = C_2(2.3 \text{ mL}) $$ $$ C_2 = \frac{(0.55 \text{ mM})(0.1 \text{ mL})}{(2.3 \text{ mL})} = 0.0239 \text{ mM} $$ The intial concentration of the substrate in the mixture is .0239 mM

4. Calculate [P] after 100 seconds using Beer-Lambert Law

The Beer-Lambert Law is given by: $ A = \epsilon \cdot l \cdot c $

where $A$ is the absorbance, $\epsilon$ is the molar extinction coefficient, $l$ is the path length, and $c$ is the concentration. We can rearrange the equation to solve for the concentration of the product [P]:

$ c = \frac{A}{\epsilon \cdot l} $

Plugging in the values:

$ c = \frac{0.995}{(99.5 \times 10^3 \text{ L mol}^{-1} \text{cm}^{-1}) \cdot (1.0 \text{ cm})} $

$ c = \frac{0.995}{99.5 \times 10^3} \text{ mol L}^{-1} = 1.0 \times 10^{-5} \text{ mol L}^{-1} $ Which can be expressed as $ c = 0.01 \text{ mM} $ Therefore the concentration of product is 0.01 mM

5. Calculating [S] after 100 seconds

Since $S \longrightarrow P$ at any time $t$, $[S]_0 = [S]_t + [P]_t$, thus $[S]_t = [S]_0 - [P]_t$

$[S]_{100} = 0.0239 \text{ mM} - 0.01 \text{ mM} = 0.0139 \text{ mM}$