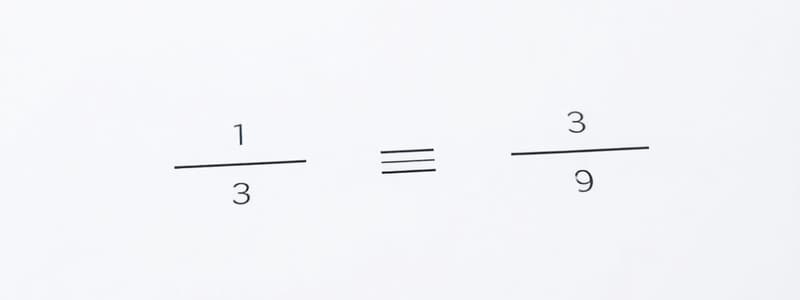Understanding Basic Fractions

Study Notes

The lecture reviews basic concepts of fractions and provides practice exercises.

A fraction represents a part of a whole, with the denominator indicating the total number of equal parts and the numerator indicating the number of parts being considered.
In a visual representation, the denominator is the total number of equal sections in a shape, and the numerator is the number of colored sections.
For example, if a shape is divided into 5 equal parts and 2 are colored, the fraction representing the colored portion is 2/5.

In an image divided into 5 parts with only 1 part colored, the fraction represented is 1/5.
For a star divided into 5 sections with 3 colored, the fraction is 3/5.
If an image has 10 sections with 4 colored, the fraction is 4/10, which simplifies to 2/5 when reduced.

Fractions on a number line follow a sequential order based on their values.
Given a number line with fractions like 1/10, 2/10, and gaps to fill before reaching 5/10, 7/10, and 9/10, students should fill in the missing fractions sequentially.
The filled number line should read: 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, culminating in 1 (or 10/10).

Simplifying fractions involves reducing them to their simplest form.
This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Example: 12/18 can be simplified by dividing both parts by 6, resulting in 2/3, which cannot be reduced further.
4/40 can be simplified by dividing both by 4, yielding 1/10.
18/24 simplifies to 3/4 when divided by 6.
20/35 simplifies to 4/7 when divided by 5.
60/12 simplifies to 5/1 (or 5) when divided by 12.

To compare or perform operations on fractions, they must have the same denominator.
This is achieved by multiplying the numerator and denominator of each fraction by a factor that results in a common denominator.
For fractions 2/5 and 3/7, the common denominator can be 35.
Convert 2/5 to 14/35 (multiply by 7) and 3/7 to 15/35 (multiply by 5).
When one denominator is a multiple of the other, only one fraction needs to be converted (e.g., 4/15 and 6/45).
Convert 4/15 to 12/45 (multiply by 3) and keep 6/45 as is.
With multiple fractions like 1/2, 1/5, and 1/3, finding the least common multiple (LCM) is efficient, such as 30.
Convert 1/2 to 15/30, 1/5 to 6/30, and 1/3 to 10/30.

To arrange fractions in ascending order, they must have a common denominator, and then be ordered by comparing their numerators.
For fractions 1/3, 1/6, 5/2, and 3/2, first convert them to have the same denominator, such as 6.
The conversions yield 2/6, 1/6, 15/6, and 9/6.
This arrangement becomes 1/6 (smallest), 2/6 (or 1/3), 9/6 (or 3/2), and 15/6 (or 5/2, largest).