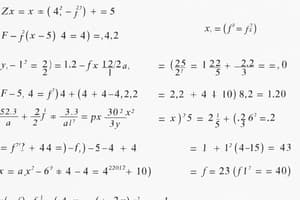Systems of Equations Quiz
50 Questions
0 Views

Choose a study mode

Play Quiz
Study Flashcards
Spaced Repetition
Chat to lesson

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the system of equations that indicates a unique solution?

  • a + b = 10 and a + 2b = 12 (correct)
  • a + b = 10 and a + b + 2b = 20
  • a + b + c = 10 and a + b + 3c = 20
  • a + b = 10 and a + b + 2c = 15

    • What characterizes the third system of equations in the provided content?

  • It has no solutions. (correct)
  • It has a unique solution.
  • It has dependent equations.
  • It has an infinite number of solutions.

    • What does the term 'redundant' imply about System 2 in the content?

  • The system has no solutions.
  • One equation is dependent on the others. (correct)
  • The equations are contradictory.
  • The system has a unique solution.

    • What results in an 'infinitely many solutions' scenario based on the systems of equations discussed?

    <p>Dependent equations that validate multiple outcomes.</p> Signup and view all the answers

    If a dog, cat, and bird were represented in an equation, which of the following statements aligns with the given information about their colors?

    <p>The bird is red.</p> Signup and view all the answers

    What is the unique solution for the cost of an apple and a banana based on the given information?

    <p>$8 for an apple, $2 for a banana.</p> Signup and view all the answers

    Which statement describes the nature of the equations derived from the purchases of the apple, banana, and cherry?

    <p>The system is non-singular.</p> Signup and view all the answers

    In the scenario where an apple, a banana, and a cherry were purchased over three days, what is the total cost for all three fruits?

    <p>$15</p> Signup and view all the answers

    Based on the second day's purchases, which equation correctly represents the transactions?

    <p>a + 2b + c = 15</p> Signup and view all the answers

    If two apples and two bananas cost $20 on the second day, what can be concluded about the overall pricing?

    <p>The cost doubles from the first day.</p> Signup and view all the answers

    Which of the following fruit price combinations correctly solves the equations derived from the three-day purchase scenario?

    <p>Apple = $3, Banana = $5, Cherry = $2.</p> Signup and view all the answers

    During the analysis of the fruit prices, what observation can be made about the relations between fruit costs across multiple days?

    <p>The prices show a constant relationship.</p> Signup and view all the answers

    What is the determinant of the matrix ( \begin{pmatrix} 5 & 1 \ -1 & 3 \end{pmatrix} )?

    <p>17</p> Signup and view all the answers

    Which of the following statements is true regarding singular and non-singular matrices?

    <p>A matrix is non-singular if its determinant is non-zero.</p> Signup and view all the answers

    What can you do with the slides distributed under the Creative Commons License?

    <p>Make copies for educational purposes with citation</p> Signup and view all the answers

    Which of the following matrices is singular?

    <p>( \begin{pmatrix} 1 &amp; 1 \ 1 &amp; 1 \end{pmatrix} )</p> Signup and view all the answers

    In the equation $y = wm x + b$, what does 'wm' represent?

    <p>The weight associated with the input variable</p> Signup and view all the answers

    What type of machine learning is shown in the given content?

    <p>Supervised learning</p> Signup and view all the answers

    Calculate the determinant of the matrix ( \begin{pmatrix} 2 & -1 \ -6 & 3 \end{pmatrix} ).

    <p>0</p> Signup and view all the answers

    Which of the following is NOT an input feature mentioned?

    <p>Time</p> Signup and view all the answers

    If a matrix has $ad - bc = 0$, what can be concluded about the matrix?

    <p>It is singular.</p> Signup and view all the answers

    What equation properly represents the relationship between features and output?

    <p>y = w1x1 + w2x2 + w3x3 + w4x4 + b</p> Signup and view all the answers

    In the visualization of wind speed vs. power output, what is the maximum power output indicated?

    <p>3500 kW</p> Signup and view all the answers

    Which formula correctly represents the output in relation to multiple features?

    <p>y = w1x1 + w2x2 + w3x3 + w4x4 + b</p> Signup and view all the answers

    What is the purpose of using weights like w1, w2, etc., in the equations?

    <p>To quantify the influence of each feature on the output</p> Signup and view all the answers

    Which of the following elements is least likely to affect the relationship described between inputs and outputs?

    <p>Advertising budget</p> Signup and view all the answers

    How can outputs be predicted if multiple input features are involved?

    <p>Through a function involving weights and input features</p> Signup and view all the answers

    What does the symbol 'b' typically represent in a linear equation?

    <p>The intercept where the line crosses the output axis</p> Signup and view all the answers

    In the context of linear regression, which option best summarizes the goal?

    <p>To predict an output variable from given input variables</p> Signup and view all the answers

    What is the determinant of the first matrix given?

    <p>16</p> Signup and view all the answers

    Which statement is true regarding singular and non-singular matrices based on the given determinants?

    <p>Matrix 1 is non-singular, and Matrix 2 is singular.</p> Signup and view all the answers

    What is the value of the determinant calculated with the elements 1, 2, and 1 in a 3x3 matrix?

    <p>2</p> Signup and view all the answers

    Which operation contributes negatively to the determinant calculation in the provided examples?

    <p>Subtracting the products of the anti-diagonals</p> Signup and view all the answers

    In the determinant calculation examples, which value is directly related to the final total?

    <p>Result from both adding and subtracting computed products</p> Signup and view all the answers

    If a matrix has a determinant of 0, it is classified as which type?

    <p>Singular</p> Signup and view all the answers

    In the computation of determinants, how many products do you evaluate in a basic 3x3 matrix scenario?

    <p>6</p> Signup and view all the answers

    Considering the first matrix, what are the values of all entries used in its determinant calculation?

    <p>5, 1, -1, 3</p> Signup and view all the answers

    Which of the following describes a non-singular system of linear equations?

    <p>It has a unique solution.</p> Signup and view all the answers

    When is a system of equations considered singular?

    <p>When two or more equations are multiples of each other.</p> Signup and view all the answers

    Which statement correctly describes the relationship between the number of solutions and linear dependence?

    <p>Linear dependent rows imply either no solutions or infinitely many solutions.</p> Signup and view all the answers

    How can you determine that a system of equations is inconsistent?

    <p>If the augmented matrix has a row that represents a false statement.</p> Signup and view all the answers

    What can be inferred about the rows of a non-singular matrix?

    <p>No row can be derived as a combination of the others.</p> Signup and view all the answers

    In the context of systems of equations, what defines a redundant equation?

    <p>An equation that adds no new information to the system.</p> Signup and view all the answers

    Which of the following conditions will ensure a system of equations has infinitely many solutions?

    <p>At least two equations are combinations of one another.</p> Signup and view all the answers

    What role do constants play in determining singularity or non-singularity?

    <p>They are irrelevant; the relationships between variables matter.</p> Signup and view all the answers

    The system represented by the equations a+b+c=0, a+b+2c=0, and 2a+2b+2c=0 is characterized as:

    <p>Singular with infinitely many solutions.</p> Signup and view all the answers

    If a system of three linear equations in three variables has only one solution, what can be concluded about its matrix?

    <p>The matrix is non-singular.</p> Signup and view all the answers

    Which method can be used to test for linear dependence among rows of a matrix?

    <p>Verifying if the determinant is zero.</p> Signup and view all the answers

    Which of the following describes a possible outcome of a system that has a dependent row?

    <p>An infinite number of solutions.</p> Signup and view all the answers

    What is the geometric interpretation of a non-singular system of equations?

    <p>Several lines intersecting at one unique point.</p> Signup and view all the answers

    Study Notes

    • Slides distributed under Creative Commons License
    • DeepLearning.ai provides slides for educational purposes only
    • Commercial use or distribution prohibited
    • Copying and distribution allowed for educational purposes with proper citation of DeepLearning.AI as the source

    Linear Algebra - Week 1

    • Course topic: Math for Machine Learning
    • Subtopic: Linear algebra

    System of Linear Equations

    • Subtopic: Linear Algebra Applied I

    Machine Learning

    • Depicts graphical representations of machine learning concept
    • Includes diagrams of neural networks, data points on a graph, and document icons.

    Machine Learning Specialization

    • Advertisement for DeepLearning.AI's Machine Learning Specialization course
    • Includes an interactive robot character and human instructors, along with call to enroll.

    Linear Algebra and Machine Learning

    • Topic: Linear Regression
    • Subtopic: Supervised Machine Learning
    • Input data flows into the process
    • Output is generated from the input
    • Wind speed is cited as an input example
    • Electrical power output is an example of an output

    Linear Algebra and Machine Learning

    • Input: Wind speed
    • Output: Power output

    Linear Algebra and Machine Learning

    • Input-output relationship illustrated on a graph displaying a plot of wind speed against power.
    • The plot is a line representing a linear regression model.

    Linear Algebra and Machine Learning

    • Input/output example illustrated with wind speed and power output.

    Linear Algebra and Machine Learning

    • Input features mentioned: wind speed, temperature
    • Output example: power output

    Linear Algebra and Machine Learning

    • Input features: wind speed, temperature, and pressure, humidity
    • Output feature: power output

    Linear Algebra and Machine Learning

    • Features are introduced: wind speed, temperature, pressure, humidity, and other features
    • Output/target output
    • Formula introduced: y=Wx +b

    Linear Algebra and Machine Learning

    • Input features (variables): wind speed, temperature, pressure, humidity, others
    • Output/target: power output

    Linear Algebra and Machine Learning

    • A system of linear equations is presented in a matrix format.
    • This shows the relationship between multiple inputs and a single output or target.

    Linear Algebra Applied II - System of Linear equations

    Linear Algebra and Machine Learning

    • Illustrates graphical relationship
    • Input/output relationship using a graph

    Linear Algebra and Machine Learning

    • The concepts of input and output is further developed.
    • Features such as wind speed and temperature are described alongside output quantity, power output.

    Linear Algebra and Machine Learning

    • Input features and their types are explicitly shown
    • Features: wind speed, temperature, pressure, humidity, other features
    • Target/output: Power ouput

    Linear Algebra and Machine Learning

    • A matrix is presented showing the mathematical relationship between variables and their output/target

    Linear Algebra and Machine Learning

    • System of linear equations formalized as an algebraic series of equations

    System of Linear Equations

    • Plan for the week
    • Includes subtopics: common vector and matrix operations; Questions (to-do list), end of week

    Plan for the Week

    • Subtopics: systems of linear equations;
    • representing systems as vectors and matrices, computing determinants

    Check your Knowledge

    • The problem involves three statements as equations.
    • Statements relating linear algebra, calculus, and probability scores
    • Mathematical representations of real-world information are presented

    Check your Knowledge

    • Questions regarding weights, features, and targets in a linear equation system
    • Values for the targets are provided.

    Check your Knowledge

    • Is the system singular or non-singular?
    • Questions: solving the system of equations, matrix representation, calculation of determinant

    What to Expect

    • Indicates the steps and learning stages to complete.
    • Lists steps in the learning process

    Systems of Sentences

    • System 1: complete and non-singular
    • System 2: redundant and singular
    • System 3: contradictory and singular

    Systems of Sentences

    • Examples of different systems of sentences
    • Includes complete, redundant, and contradictory sentence systems

    Quiz: Systems of Sentences

    • The quiz question has statements describing relationships between the dog, cat and a bird(or other objects).
    • Questions regarding the color of the bird and singularity of the system.

    Solution: Systems of Information

    • Finding the color of the bird
    • The system is determined as being non-singular

    System of Equations

    • Converting sentences to equations through numerical representation.
    • Example: the price of an apple and a banana cost $10

    Quiz: Systems of Equations 1

    • Statements regarding buying fruits
    • The quiz requires calculating the price of each for the fruits purchased

    Solution: Systems of Equations 1

    • The solution represents the calculation for the fruit prices based on the provided information

    Quiz: Systems of Equations 2

    • Real-world problem
    • The quiz statement describes purchasing different combinations of fruits (apples, bananas, and cherries) at different costs

    Solution: Systems of Equations 2

    • Showing the systems of linear equations related to the problem

    Quiz: Systems of Equations 3

    • Statements regarding apples and bananas prices based on purchasing scenarios
    • The price of each fruit(apple, banana) needs to be calculated

    Solution: Systems of Equations 3

    • Solution based on the provided data for prices of apples and bananas.

    Quiz: Systems of Equations 4

    • Statements show buying scenarios with fruits (apple, banana cost)
    • The quiz task for calculating the fruit cost.

    Solution: Systems of Equations 4

    • Statements about the buy scenarios for fruits (apple, banana)
    • The solution is a contradiction and no solution is possible

    Systems of Equations

    • A set of equations (variables: a, b) are presented.
    • Each system is analyzed and a proper classification is made based on multiple properties.
    • The types presented include unique solution, infinite solutions, and no solution

    Quiz: More Systems of Equations

    • Three systems of equations are described, each containing three variables (a, b, and c).
    • Each system of linear equations is to be properly solved and classified

    Solutions: More Systems of Equations

    • Solutions to the three systems of equations are shown and classified
    • Examples include infinitely many solutions, no solutions, and infinite solutions

    What is a Linear Equation?

    • Distinguishes linear and non-linear equations
    • Example equations from both categories illustrated.

    System of Linear Equations

    • Describes systems of equations as lines and planes

    Linear equation → line

    • Represents linear equations graphically as lines on a coordinate plane
    • Illustrates unique solutions from the intersection of lines

    Linear equation → line

    • Representation of linear equations as a set of lines or a plane within a 3d coordinate

    Linear equation → line

    • Unique graphical representation of linear equations as lines

    Linear equation → line

    • Graphical representations of linear equations as lines, including possible outcomes (unique solution)

    Systems of equations as lines

    • Linear equations as lines on a coordinate plane
    • Different possible outcomes presented (unique solution, infinite solutions, no solutions)

    Quiz

    • The problem involves plotting different systems of equations

    Solution

    • The problem asks which plot is the best fit for two linear equations

    Linear equation in 3 variables as a plane

    • The geometrical interpretation of a linear equation in three variables

    Linear equation in 3 variables as a plane

    • Linear equation in three variables illustrated

    System 1

    • Set of equations are presented
    • Further geometrical description using diagram

    System 2

    • Equations shown
    • Illustration shown

    System 3

    • Equations shown
    • Illustrations shown

    System of Linear Equations

    • Discusses the concept of singularity.

    Systems of equations as lines

    • Explains systems of linear equations as lines or planes
    • Shows different scenarios (unique solution, infinite solutions, no solutions)

    Systems of equations as lines

    • Explains how systems of linear equations can represent lines

    Systems of equations as matrices

    • Explains systems of equations as matrices with singular and non-singular matrices given.

    Constants don't matter for singularity

    • Explains that the constant values do no affect the singular nature of a system

    Constants don't matter for singularity

    • Describes how constant values in a series of equations do not affect the singular or non-singular nature of a matrix

    Constants don't matter for singularity

    • Explains the properties of linear equations, including singular and non-singular properties

    Quiz: Determinants

    • Determines determinants for different matrices

    Solution: Determinants

    • Solutions for the previously mentioned quiz on calculating determinants for different matrices.

    The determinant

    • Illustration of the determinant in a 3x3 matrix.
    • Illustrates calculations for different diagonals of the matrix.

    Conclusion

    • Summary of the main concepts covered in the study material.

    Studying That Suits You

    Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

    Quiz Team

    Related Documents

    Math for Machine Learning Linear Algebra - Week 1 PDF

    Description

    Test your understanding of systems of equations with this quiz. Explore concepts such as unique solutions, characteristics of systems, and scenarios leading to infinite solutions. Challenge yourself to identify and analyze different types of equations.

    More Like This

    Use Quizgecko on...
    Browser
    Open
    Browser
    Browser