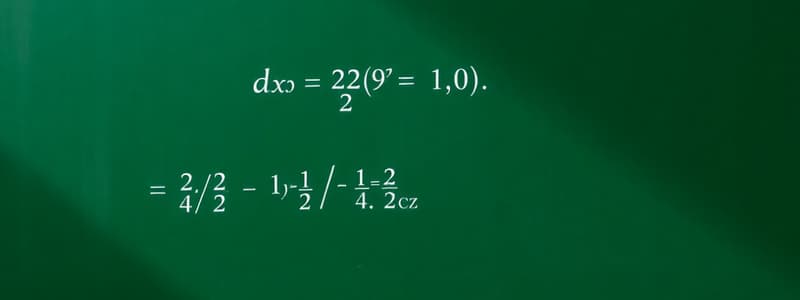Podcast
Questions and Answers
In the Simpson's rule implementation, what does h represent?
In the Simpson's rule implementation, what does h represent?
- The sum of odd terms.
- The number of sub-intervals.
- The interval size. (correct)
- The sum of even terms.
What is the purpose of the Table function in the provided code snippet?
What is the purpose of the Table function in the provided code snippet?
- To calculate and store the values of $f(x)$ at each point.
- To determine the step size $h$.
- To generate a list of $x$ values within the interval $[a, b]$. (correct)
- To compute the definite integral of $f(x)$.
What role do sumodd and sumeven play in the Simpson's rule calculation?
What role do sumodd and sumeven play in the Simpson's rule calculation?
- `sumodd` stores the sum of odd number of intervals, while `sumeven` stores the sum of even number of intervals.
- `sumodd` calculates the sum of $f(x)$ at even indices, while `sumeven` calculates the sum at odd indices.
- `sumodd` and `sumeven` accumulate the weighted sums of function evaluations at odd and even indices, respectively. (correct)
- `sumodd` calculates the sum of $x$ coordinates with odd indices, while `sumeven` calculates the sum of $x$ coordinates with even indices.
How is the Simpson's rule estimate (Sn) calculated in the given code?
How is the Simpson's rule estimate (Sn) calculated in the given code?
What is the purpose of the line f[x_] := 1/x; in the Simpson's rule implementation?
What is the purpose of the line f[x_] := 1/x; in the Simpson's rule implementation?
What do a and b represent in the context of the Simpson's rule code?
What do a and b represent in the context of the Simpson's rule code?
What is being computed by the line in = Integrate[1/x, {x, 1, 2}]?
What is being computed by the line in = Integrate[1/x, {x, 1, 2}]?
For the given function $f(x) = 1/x$, what is the purpose of calculating Abs[Sn - in]?
For the given function $f(x) = 1/x$, what is the purpose of calculating Abs[Sn - in]?
In the context of numerical integration, what is the significance of increasing the number of subintervals (n) in Simpson's rule?
In the context of numerical integration, what is the significance of increasing the number of subintervals (n) in Simpson's rule?
Which of the following best describes a limitation of Simpson's rule for numerical integration?
Which of the following best describes a limitation of Simpson's rule for numerical integration?
What type of numerical integration method is Simpson's rule?
What type of numerical integration method is Simpson's rule?
Assume a function $f(x)$ is approximated using Simpson's rule with $n$ subintervals. If the number of subintervals is doubled to $2n$, how is the accuracy of the approximation generally affected?
Assume a function $f(x)$ is approximated using Simpson's rule with $n$ subintervals. If the number of subintervals is doubled to $2n$, how is the accuracy of the approximation generally affected?
What condition must be satisfied by the number of subintervals (n) for Simpson's rule to be applicable?
What condition must be satisfied by the number of subintervals (n) for Simpson's rule to be applicable?
If the exact value of an integral is 5.0, and Simpson's rule gives an approximation of 4.8, what is the absolute error?
If the exact value of an integral is 5.0, and Simpson's rule gives an approximation of 4.8, what is the absolute error?
Which of the following is the primary reason Simpson's rule is generally more accurate than the trapezoidal rule for numerical integration?
Which of the following is the primary reason Simpson's rule is generally more accurate than the trapezoidal rule for numerical integration?
Suppose you are using Simpson's rule to approximate the integral of a function. Which of the following actions would likely improve the accuracy of your approximation the most?
Suppose you are using Simpson's rule to approximate the integral of a function. Which of the following actions would likely improve the accuracy of your approximation the most?
What is the weight applied to the function value at the endpoints ($f(a)$ and $f(b)$) in Simpson's rule?
What is the weight applied to the function value at the endpoints ($f(a)$ and $f(b)$) in Simpson's rule?
In the Simpson's rule algorithm, what happens if the number of subintervals is not an even number?
In the Simpson's rule algorithm, what happens if the number of subintervals is not an even number?
Compared to other numerical integration techniques, what is a key advantage of Simpson's rule?
Compared to other numerical integration techniques, what is a key advantage of Simpson's rule?
What is the effect of a singularity within the interval of integration when using Simpson's rule?
What is the effect of a singularity within the interval of integration when using Simpson's rule?
Flashcards
Simpson's Rule
Simpson's Rule
A numerical integration technique to approximate the definite integral of a function.
Left endpoint (a)
Left endpoint (a)
The starting point of the interval over which the integration is performed.
Right endpoint (b)
Right endpoint (b)
The ending point of the interval over which the integration is performed.
Number of subintervals (n)
Number of subintervals (n)
Signup and view all the flashcards
Subinterval width (h)
Subinterval width (h)
Signup and view all the flashcards
x values (y)
x values (y)
Signup and view all the flashcards
Function f(x)
Function f(x)
Signup and view all the flashcards
Sumodd
Sumodd
Signup and view all the flashcards
Sumeven
Sumeven
Signup and view all the flashcards
Simpson estimate (Sn)
Simpson estimate (Sn)
Signup and view all the flashcards
Integrate function
Integrate function
Signup and view all the flashcards
Absolute error
Absolute error
Signup and view all the flashcards
Study Notes
Simpson's Rule Implementation
- A script implementing Simpson's rule for numerical integration is presented.
- The script calculates the Simpson estimate and the absolute error compared to the true value of the integral.
- The left end point of the interval is inputted and assigned to variable a.
- The right end point of the interval is inputted and assigned to variable b.
- The number of subintervals is inputted and assigned to variable n.
- The width of each subinterval is calculated as h = (b - a) / n.
- A table y of x-values at each subinterval is created using
Table[a + i*h, {i, 1, n}]. - The function f(x) is defined as 1/x.
- Variables
sumoddandsumevenare initialized to 0, to accumulate sums for odd and even indexed subintervals, respectively. - A
Forloop iterates through odd indices, calculating the sum of4 * f(x)at each odd point y[[i]] and accumulating it insumodd. - A
Forloop iterates through even indices, calculating the sum of2 * f(x)at each even point y[[i]] and accumulating it insumeven. - The Simpson's rule estimate
Snis calculated using the formula(h/3) * ((f[x] /. x -> a) + N[sumodd] + N[sumeven] + (f[x] /. x -> b)). - The Simpson estimate is printed for a specific value of n.
- The variable
incalculates the definite integral of 1/x from 1 to 2. - The true value of the integral is printed.
- The absolute error between the Simpson's rule estimate
Snand the true valueinis then calculated and printed.
Error and True Value Calculations
- For n = 10, the Simpson estimate generated is {1., 0.5, 1.}.
- An error message indicates an invalid integration variable or limits specified as 'Integrate: Invalid integration variable or limit(s) in {{1, 2, 1}, 1, 2}.'
- The true value calculation displays an integral expression: integral from 1 to 1/2 to 1 of d{1,2,1}.
- The absolute error is expressed as
Abs[1 - integral from 1 to 1/2 to 1]. - Additional absolute error terms are given by
Abs[0.5 - integral from 1 to 1/2 to 1]andAbs[1 - integral from 1 to 1/2 to 1].
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.