Podcast
Questions and Answers
What is the domain of a function?
What is the domain of a function?
- The steepness of a line (correct)
- The set of all possible input values
- The set of all possible output values
- The point where the graph crosses the y-axis
What is the range of a function?
What is the range of a function?
- The point where the graph crosses the x-axis
- The set of all possible output values (correct)
- The set of all possible input values
- The horizontal extent of the graph
Which property of logarithms allows you to simplify $\log(ab)$?
Which property of logarithms allows you to simplify $\log(ab)$?
- Quotient Rule (correct)
- Change of Base Rule
- Product Rule
- Power Rule
Which property of logarithms allows you to simplify $\log(\frac{a}{b})$?
Which property of logarithms allows you to simplify $\log(\frac{a}{b})$?
What is the value of $\log_b(1)$ for any base $b$?
What is the value of $\log_b(1)$ for any base $b$?
If $\ln(x) = y$, then $e^y$ equals what?
If $\ln(x) = y$, then $e^y$ equals what?
What is the inverse function of $f(x) = log_b(x)$?
What is the inverse function of $f(x) = log_b(x)$?
In the exponential function $f(x) = ab^x$, what does 'a' represent?
In the exponential function $f(x) = ab^x$, what does 'a' represent?
Flashcards
Expanding Logarithms
Expanding Logarithms
Use logarithm properties (product, quotient, power) to expand expressions, treating powers as factors.
Logarithm Properties
Logarithm Properties
Use properties of logarithms to find the exact value of the logarithm without using a calculator.
Exponential Model
Exponential Model
An exponential model is a function of the form f(x) = ab^x that fits a given set of data points.
Exponential Decay Model
Exponential Decay Model
Signup and view all the flashcards
Solving Logarithmic Equations
Solving Logarithmic Equations
Signup and view all the flashcards
Exponential-Logarithmic Conversion
Exponential-Logarithmic Conversion
Signup and view all the flashcards
Solving Equations with Natural Logs
Solving Equations with Natural Logs
Signup and view all the flashcards
Solving Equations with Logarithms
Solving Equations with Logarithms
Signup and view all the flashcards
Exponential Decay Model Formulation
Exponential Decay Model Formulation
Signup and view all the flashcards
Calculate future population
Calculate future population
Signup and view all the flashcards
Study Notes
- An inference is drawing conclusions from available evidence
- In logic, a rule of inference is a logical form that takes premises, analyzes their syntax, and returns a conclusion
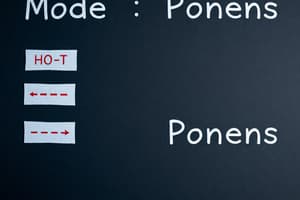
Modus Ponens
- If P then Q.
- P is true.
- Therefore, Q is true.
- Example: If it's raining, there are clouds. It's raining. Therefore, there are clouds.
Modus Tollens
- If P then Q.
- Q is false.
- Therefore, P is false.
- Example: If it's raining, there are clouds. There are no clouds. Therefore, it is not raining.
Hypothetical Syllogism
- If P then Q.
- If Q then R.
- Therefore, if P then R.
- Example: If I study, I will pass the exam. If I pass, I'll get a good job. Therefore, if I study, I'll get a good job.
Disjunctive Syllogism
- P or Q is true.
- P is false.
- Therefore, Q is true.
- Example: I'm either home or at work. I'm not home. Therefore, I am at work.
Addition
- P is true.
- Therefore, P or Q is true.
- Example: It's raining. Therefore, it's raining or snowing.
Simplification
- P and Q are true.
- Therefore, P is true.
- Example: It's raining and snowing. Therefore, it's raining.
Conjunction
- P is true.
- Q is true.
- Therefore, P and Q are true.
- Example: It's raining. It's snowing. Therefore, it's raining and snowing.
Resolution
- P or Q is true.
- Not P or R is true.
- Therefore, Q or R is true.
- Example: I'm either home or at work. I'm either not home or on vacation. Therefore, I'm either at work or on vacation.
Quantifiers
Universal Generalization (UG)
- If $P(a)$ is true for any arbitrary element $a$ of the domain, then $\forall x P(x)$ is true.
Universal Instantiation (UI)
- If $\forall x P(x)$ is true, then $P(a)$ is true for any element $a$ of the domain.
Existential Generalization (EG)
- If $P(a)$ is true for some element $a$ of the domain, then $\exists x P(x)$ is true.
Existential Instantiation (EI)
- If $\exists x P(x)$ is true, then $P(a)$ is true for some element $a$ of the domain.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Explore rules of inference like Modus Ponens, Modus Tollens, and Hypothetical Syllogism. Learn how to draw logically sound conclusions from premises. Understand deductive reasoning with examples.