Podcast
Questions and Answers
¿Qué técnica se utiliza para resolver ecuaciones cuadráticas?
¿Qué técnica se utiliza para resolver ecuaciones cuadráticas?
¿En qué consiste el proceso de factorizar una ecuación cuadrática?
¿En qué consiste el proceso de factorizar una ecuación cuadrática?
¿Qué tipo de ecuaciones se pueden representar con el formato ax^2 + bx + c = 0?
¿Qué tipo de ecuaciones se pueden representar con el formato ax^2 + bx + c = 0?
¿Qué aspecto de las ecuaciones se considera al aplicar técnicas de factorización?
¿Qué aspecto de las ecuaciones se considera al aplicar técnicas de factorización?
Signup and view all the answers
¿Cuál es el propósito principal de factorizar una ecuación cuadrática?
¿Cuál es el propósito principal de factorizar una ecuación cuadrática?
Signup and view all the answers
¿Cuál es la propiedad única de cada término en la ecuación dada en la primera parte del texto?
¿Cuál es la propiedad única de cada término en la ecuación dada en la primera parte del texto?
Signup and view all the answers
¿Qué número se puede sustituir en lugar de las variables en la secuencia para que la igualdad sea verdadera?
¿Qué número se puede sustituir en lugar de las variables en la secuencia para que la igualdad sea verdadera?
Signup and view all the answers
¿Cómo se puede resolver una ecuación de primer grado si ni la suma ni la resta son útiles?
¿Cómo se puede resolver una ecuación de primer grado si ni la suma ni la resta son útiles?
Signup and view all the answers
¿Qué recomendación se da para verificar el trabajo realizado al resolver ecuaciones?
¿Qué recomendación se da para verificar el trabajo realizado al resolver ecuaciones?
Signup and view all the answers
¿Qué se sugiere hacer si se intentan varios métodos sin éxito para resolver una ecuación?
¿Qué se sugiere hacer si se intentan varios métodos sin éxito para resolver una ecuación?
Signup and view all the answers
Study Notes
Equations form the basis of algebraic thinking, where we represent relationships between variables using mathematical symbols. They can range from simple expressions like (x + 5 = 8), which requires us to solve for x by finding what value can replace it so both sides are equal, to more complex ones such as quadratic equations of the form [ax^2+bx+c=0]which require different techniques depending on their degree.
In this section, we'll explore several aspects of equations including factoring quadratic equations, solving first-degree equations, applications of linear and quadratic equations, graphing quadratic equations, and solving second-degree equations.
Factoring Quadratic Equations
Factoring is one method used to solve quadratics. For example, consider the equation [(a)(u) = (ab)], where u is the product of two numbers a and b. We can see that factoring out the common factor gives us ((a)(u) - ab = 0).
For instance, let's take the equation (ax^2 + bx + c = 0). By taking a close look at this expression, you may notice that there is nothing special about all these terms — they just happen to come together here! So if I want to make them into factors, I need some kind of pattern among these three values. One possible way would be arranging them based on their coefficients; i.e., having each term with coefficient zero followed by two consecutive nonzero integers. Thus we have: [ \begin{aligned} & ax^2 \ & + bx\ & + cx \end{aligned}= \begin{aligned} & ax \ & bx\ & cx \end{aligned}]Next, note how every term has its own unique property—the first row consists solely of squares while every other row contains only cubes? But wait! What about when dealing with variables greater than six? Well...you guessed right. There will always exist some number N such that replacing any single variable within this sequence with integer N makes it true overall.
The main idea behind this method lies in breaking down larger quantities into smaller 'parts', hoping that those parts somehow fit together nicely. And sometimes good things really do happen just because they happened.
Solving First-Degree Equations
Solving a first-degree equation involves finding the value of a variable that satisfies the given equality. This can often be done through substitution, in which case you simply plug in your answer to find whether it works or not. However, if neither subtraction nor addition solves our problem, division might help. If necessary, rearrange expressions before dividing until everything is neatly arranged. Afterward, check your work by performing reverse operations such as adding back numbers taken away during earlier stages.
If still stuck after trying several methods without success, try transforming to another system instead. Sometimes solutions appear under disguise! For example, changing signs around could reveal hidden properties allowing easy calculation otherwise unseen. Remember though: practice makes perfect! Don't worry too much about early struggles – keep working at it till mastery comes naturally.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
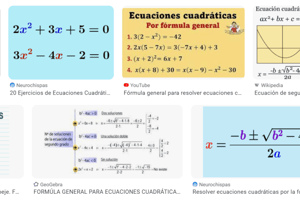
Explora varios aspectos sobre la resolución de ecuaciones, incluyendo el factorización de ecuaciones cuadráticas, solución de ecuaciones de primer grado, aplicaciones de ecuaciones lineales y cuadráticas, graficación de ecuaciones cuadráticas y solución de ecuaciones de segundo grado.
