Podcast
Questions and Answers
Which regular expression accurately describes the set of strings 'w' that begin with '1' and end with '0', encompassing any characters in between?
Which regular expression accurately describes the set of strings 'w' that begin with '1' and end with '0', encompassing any characters in between?
- 10*
- Σ*1Σ*0Σ*
- 1Σ*0 (correct)
- 1Σ*
Which regular expression defines the set of strings 'w' containing at least three occurrences of '1'?
Which regular expression defines the set of strings 'w' containing at least three occurrences of '1'?
- (Σ1){3,}
- 111
- Σ*1Σ*1Σ*1 (correct)
- Σ*1Σ*1Σ*1Σ*
Which regular expression matches strings 'w' where every odd position is a '1'?
Which regular expression matches strings 'w' where every odd position is a '1'?
- (1Σ)*(ε ∪ 1) (correct)
- (Σ1)*
- 1(Σ1)*
- (1Σ)*
Which of the following regular expressions describes a language that includes strings containing at least two '0's and at most one '1'?
Which of the following regular expressions describes a language that includes strings containing at least two '0's and at most one '1'?
Which regular expression accurately represents the set of all strings except for '11' and '111'?
Which regular expression accurately represents the set of all strings except for '11' and '111'?
Which of the following statements accurately describes the difference between regular languages and non-regular languages?
Which of the following statements accurately describes the difference between regular languages and non-regular languages?
Consider a language consisting of strings that start with 'a' and are followed by any number of 'b's. Which regular expression accurately represents this language?
Consider a language consisting of strings that start with 'a' and are followed by any number of 'b's. Which regular expression accurately represents this language?
Which of the following is true regarding Kleene Star closure and Plus operation?
Which of the following is true regarding Kleene Star closure and Plus operation?
Given a regular expression (ab)*, which of the following strings is NOT generated by this expression?
Given a regular expression (ab)*, which of the following strings is NOT generated by this expression?
What is the relationship between a* and a+?
What is the relationship between a* and a+?
Which of the following regular expressions is equivalent to (a+a*)?
Which of the following regular expressions is equivalent to (a+a*)?
Given the relationship a+ = a a*, what language does a a* represent?
Given the relationship a+ = a a*, what language does a a* represent?
Which regular expression is equivalent to one or more occurrences of 'ab'?
Which regular expression is equivalent to one or more occurrences of 'ab'?
Which regular expression accurately represents the language of all words consisting of one 'b' followed by any number of 'a's (including zero) over the alphabet ∑ = {a, b}?
Which regular expression accurately represents the language of all words consisting of one 'b' followed by any number of 'a's (including zero) over the alphabet ∑ = {a, b}?
Which of the following regular expressions defines a language that includes strings with an even number of 'b's, where the alphabet ∑ = {b}?
Which of the following regular expressions defines a language that includes strings with an even number of 'b's, where the alphabet ∑ = {b}?
Consider the regular expressions r1 = a* + b* and r2 = (a + b)*. Which statement correctly describes the languages generated by these expressions?
Consider the regular expressions r1 = a* + b* and r2 = (a + b)*. Which statement correctly describes the languages generated by these expressions?
Which regular expression correctly represents a language that contains all strings over Σ = {x} with at least one 'x'?
Which regular expression correctly represents a language that contains all strings over Σ = {x} with at least one 'x'?
Let ∑ = {a, b}. What language is described by the regular expression a(bb)*a?
Let ∑ = {a, b}. What language is described by the regular expression a(bb)*a?
Given the alphabet ∑ = {a}, which regular expression defines the language of all strings with an odd number of 'a's?
Given the alphabet ∑ = {a}, which regular expression defines the language of all strings with an odd number of 'a's?
Which regular expression cannot represent the language L = {a, aa, aaa, ...}?
Which regular expression cannot represent the language L = {a, aa, aaa, ...}?
According to the definition, which of the following is NOT a regular expression, assuming 'a' and 'b' are symbols from the alphabet?
According to the definition, which of the following is NOT a regular expression, assuming 'a' and 'b' are symbols from the alphabet?
How would you represent a C identifier (variable name) using a regular expression, where an identifier must start with a letter (L) or underscore (_), followed by any combination of letters, digits (D), or underscores?
How would you represent a C identifier (variable name) using a regular expression, where an identifier must start with a letter (L) or underscore (_), followed by any combination of letters, digits (D), or underscores?
Which regular expression defines a language consisting of strings that have odd number of 'a's or even number of 'b's, where ∑ = {a, b}?
Which regular expression defines a language consisting of strings that have odd number of 'a's or even number of 'b's, where ∑ = {a, b}?
Flashcards
Regular Language
Regular Language
A language generated by a regular expression.
Regular Expressions (RE)
Regular Expressions (RE)
Expressions used to denote formal languages.
RE Limitations
RE Limitations
Not all formal languages can be described by regular expressions.
Kleene Star Closure
Kleene Star Closure
Signup and view all the flashcards
PLUS Operation (+)
PLUS Operation (+)
Signup and view all the flashcards
Key Difference: * vs +
Key Difference: * vs +
Signup and view all the flashcards
a* Example
a* Example
Signup and view all the flashcards
a+ Example
a+ Example
Signup and view all the flashcards
Arithmetic Operators
Arithmetic Operators
Signup and view all the flashcards
Assignment Operators
Assignment Operators
Signup and view all the flashcards
Increment/Decrement Operators
Increment/Decrement Operators
Signup and view all the flashcards
Logical Operators
Logical Operators
Signup and view all the flashcards
Relational Operators
Relational Operators
Signup and view all the flashcards
Kleene Star (*)
Kleene Star (*)
Signup and view all the flashcards
a*
a*
Signup and view all the flashcards
a+
a+
Signup and view all the flashcards
a* + b*
a* + b*
Signup and view all the flashcards
(a + b)*
(a + b)*
Signup and view all the flashcards
a b*
a b*
Signup and view all the flashcards
(aa)*
(aa)*
Signup and view all the flashcards
a(aa)*
a(aa)*
Signup and view all the flashcards
Study Notes
- A regular language is generated by a regular expression.
- Regular expressions denote formal languages in a precise way.
- Regular expressions is similar to arithmetic expressions.
- Not all formal languages can be described by regular expressions.
- Languages describable by regular expressions are "regular languages".
- Languages not describable by regular expressions are "non-regular languages".
- A language can have multiple regular expressions.
Kleene Star Closure
a*represents zero or more occurrences of 'a':{^, a, aa, aaa, aaaa, ...}.
PLUS Operation (+)
a+represents one or more occurrences of 'a':{a, aa, aaa, aaaa, ...}.- It is the same as Kleene Star Closure except that it does not generate null string.
a* = ^ + a+a+ = a a*- L1 =
{^, a, aa, aaa, ...}can be expressed asa*. - L2 =
{a, aa, aaa, aaaa, ...}can be expressed asa+. a+,aa*, anda*agenerate L2.
Recursive Definition of Regular Expression
- Every letter of Σ (including ^) is a regular expression.
- If r1 and r2 are regular expressions, then
(r1),r1 r2,r1 + r2, andr1*are also regular expressions. - Nothing else is a regular expression.
Examples of Regular Expressions
- L =
{^, x, xx, xxx,...}can be written asx*. - L =
{x, xx, xxx,...}can be expressed asx+. r1 = a*+b*does not generate a string of concatenated a and b, whiler2 = (a+b)*does.- Given Σ =
{a, b}, language of all words having one 'a' followed by any number of b’s (may be no b’s at all) can be defined bya b*ora (^ + b+). - If the statement of the above language did not contain the part “may be no b’s at all”, then we would have written its regular expression as a b+.
- Given Σ =
{a}, the language of all words having an even number of a’s can be defined by(aa)*or^ + (aa)+. - The language of all words having an odd number of a’s can be defined by
a (aa)*or(aa)* a.
Regular Expressions for Identifiers and Operators
- Identifiers in C must start with a letter or underscore, followed by letters, digits, or underscores.
- Let L =
[a-z A-Z]and D =[0-9]. - Regular expression for identifiers:
(L | _ ) (L | _ | D)* - Arithmetic Operators:
(+ | - | * | / | %) - Assignment/Arithmetic Assignment Operators:
(+ | - | * | / | % | ϵ) = - Increment/Decrement Operators:
(++| - -) - Logical Operators:
(&&| || | !) - Relational Operators:
(= = | != | < | <= | > | >=)
Examples of Regular Expressions
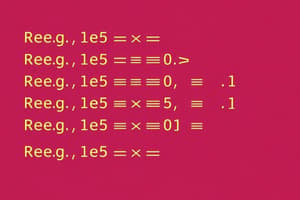
{w| w begins with a 1 and ends with a 0}:1Σ∗0{w| w contains at least three 1s}:Σ∗1Σ∗1Σ∗1Σ∗{w| w contains the substring 0101, i.e., w = x0101y for some x and y}:Σ∗0101Σ∗{w| w has length at least 3 and its third symbol is a 0}:ΣΣ0Σ∗{w| w starts with 0 and has odd length, or starts with 1 and has even length}:(0 ∪ 1Σ)(ΣΣ)∗{w| w doesn’t contain the substring 110}:0∗(10+)∗1∗{w| the length of w is at most 5}:(ε ∪ Σ)5{w| w is any string except 11 and 111}:ε ∪ Σ ∪ 0Σ ∪ 10 ∪ 0ΣΣ ∪ 10Σ ∪ 110 ∪ Σ3 Σ+{w| every odd position of w is a 1}:(1Σ)∗(ε ∪ 1){w| w contains at least two 0s and at most one 1}:00+ ∪ 100+ ∪ 0+ 10+ ∪ 00+1{ε, 0}:0 ∪ ε{w| w contains an even number of 0s, or contains exactly two 1s}:1∗(01∗01∗)∗ ∪ 0∗10∗10∗- The empty set:
∅ - All strings except the empty string:
Σ+
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Test your knowledge of regular expressions. Questions cover matching specific string patterns, occurrences of characters, odd position matching, Kleene star closure, and the difference between regular and non-regular languages. Regular expressions are a powerful tool for pattern matching in computer science.
![[04/Volkhov/10]](https://images.unsplash.com/photo-1543386576-bfb043f10f6b?ixid=M3w0MjA4MDF8MHwxfHNlYXJjaHwxM3x8c2ltcGxlJTIwcGFzdCUyMHRlbnNlJTIwcmVndWxhciUyMHZlcmJzJTIwaXJyZWd1bGFyJTIwdmVyYnMlMjBFbmdsaXNoJTIwYW5kJTIwU3BhbmlzaHxlbnwxfDB8fHwxNzA1MTU1MDY0fDA&ixlib=rb-4.0.3&w=300&fit=crop&h=200&q=75&fm=webp)
![[04/Volkhov/12]](https://images.unsplash.com/photo-1606241018160-4985a8ab5dec?ixid=M3w0MjA4MDF8MHwxfHNlYXJjaHw5fHxUaGUlMjBTbmFrZSUyMGFuZCUyMHRoZSUyME1pcnJvciUyMHN0b3J5JTIwYW5hbHlzaXMlMjBsaXRlcmF0dXJlJTIwdGhlbWUlMjBleHBsb3JhdGlvbnxlbnwxfDB8fHwxNzA1MzM1NDMwfDA&ixlib=rb-4.0.3&w=300&fit=crop&h=200&q=75&fm=webp)
