Podcast
Questions and Answers
What is the base case for the recurrence relation T(n) = 3T(n/4) + n^2?
What is the base case for the recurrence relation T(n) = 3T(n/4) + n^2?
- T(n)
- T(n/4)
- T(0)
- T(1) (correct)
The recursion tree method is a technique used to solve recurrence relations.
The recursion tree method is a technique used to solve recurrence relations.
True (A)
What is the total number of nodes at level 'i' in the recursion tree?
What is the total number of nodes at level 'i' in the recursion tree?
3^i
What is the recurrence relation for the given problem?
What is the recurrence relation for the given problem?
The impact of each node at level 'i' on the recurrence relation is ______.
The impact of each node at level 'i' on the recurrence relation is ______.
Match the following concepts to their descriptions:
Match the following concepts to their descriptions:
The recursion tree method helps visualize the recursive calls made in a problem.
The recursion tree method helps visualize the recursive calls made in a problem.
What is the base case for the recurrence relation?
What is the base case for the recurrence relation?
The impact of each node in the recursion tree at layer i is ______
The impact of each node in the recursion tree at layer i is ______
Match the following terms with their corresponding values in the recursion tree method:
Match the following terms with their corresponding values in the recursion tree method:
What is the initial step we take to prove that a time complexity function T(n) is in O(n) after introducing the claim T(n) ∈ O(n)?
What is the initial step we take to prove that a time complexity function T(n) is in O(n) after introducing the claim T(n) ∈ O(n)?
The initial induction hypothesis states that T(k) ≤ ck - d for all k < n, where c and d are constants.
The initial induction hypothesis states that T(k) ≤ ck - d for all k < n, where c and d are constants.
What is the main tool used in the provided proof to demonstrate the claim T(n) ∈ O(n)?
What is the main tool used in the provided proof to demonstrate the claim T(n) ∈ O(n)?
In the provided proof, the equation T(n) = T(⌊n/2⌋) + T(⌈n/2⌉) + 1 is used to expand the time complexity function based on the assumption that T(n) is in ______ of the size of the input n.
In the provided proof, the equation T(n) = T(⌊n/2⌋) + T(⌈n/2⌉) + 1 is used to expand the time complexity function based on the assumption that T(n) is in ______ of the size of the input n.
Match the following terms with their corresponding definitions in the provided context.
Match the following terms with their corresponding definitions in the provided context.
The recursion tree method is used to analyze the time complexity of ______ functions.
The recursion tree method is used to analyze the time complexity of ______ functions.
In the recursion tree for T(n) = 3T(n/4) + n^2, what is the value at each node at the first level?
In the recursion tree for T(n) = 3T(n/4) + n^2, what is the value at each node at the first level?
What is the base case for the recursive function T(n) = 3T(n/4) + n^2?
What is the base case for the recursive function T(n) = 3T(n/4) + n^2?
The recursion tree method can be used to analyze the time complexity of all recursive functions.
The recursion tree method can be used to analyze the time complexity of all recursive functions.
In the recursion tree for T(n) = 3T(n/4) + n^2, how many nodes are there at the second level?
In the recursion tree for T(n) = 3T(n/4) + n^2, how many nodes are there at the second level?
The recursion tree method helps to visualize how the time complexity of a recursive function ______ as the problem size decreases.
The recursion tree method helps to visualize how the time complexity of a recursive function ______ as the problem size decreases.
What is the main advantage of using the recursion tree method in analyzing time complexity?
What is the main advantage of using the recursion tree method in analyzing time complexity?
Match the following terms with their corresponding description:
Match the following terms with their corresponding description:
The recurrence relation presented in the content is T(n) = 3T(n/4) + ______
The recurrence relation presented in the content is T(n) = 3T(n/4) + ______
What is the time complexity of the algorithm represented by the recurrence relation?
What is the time complexity of the algorithm represented by the recurrence relation?
The recursion tree method is a way to visualize and solve recurrence relations.
The recursion tree method is a way to visualize and solve recurrence relations.
What does the 'n^2' term in the recurrence relation represent?
What does the 'n^2' term in the recurrence relation represent?
Match the following terms with their corresponding elements in the recursion tree method:
Match the following terms with their corresponding elements in the recursion tree method:
What is the recurrence relation for T(n)?
What is the recurrence relation for T(n)?
The impact of each node at layer 0 in the recursion tree is n^2.
The impact of each node at layer 0 in the recursion tree is n^2.
What is the value of T(1)?
What is the value of T(1)?
In the recursion tree method, the impact of each node is represented as _____ at layer 1.
In the recursion tree method, the impact of each node is represented as _____ at layer 1.
How many nodes are there at layer 2 of the recursion tree?
How many nodes are there at layer 2 of the recursion tree?
Match the following terms with their descriptions:
Match the following terms with their descriptions:
The total number of nodes in the recursion tree increases exponentially with each layer.
The total number of nodes in the recursion tree increases exponentially with each layer.
What expression represents the total work done at a layer i?
What expression represents the total work done at a layer i?
Flashcards
Recursion tree method
Recursion tree method
A visual method for analyzing the time complexity of recursive algorithms.
T(n) = 3T(n/4) + n²
T(n) = 3T(n/4) + n²
A specific recurrence relation representing time complexity in algorithms.
Node Impact Count
Node Impact Count
The contribution of each node's calculation to the overall complexity.
Layer in recursion tree
Layer in recursion tree
Signup and view all the flashcards
Impact at layer 0
Impact at layer 0
Signup and view all the flashcards
Base Case
Base Case
Signup and view all the flashcards
Depth of Recursion Tree
Depth of Recursion Tree
Signup and view all the flashcards
Subproblems in Recursion
Subproblems in Recursion
Signup and view all the flashcards
Work Done at Each Level
Work Done at Each Level
Signup and view all the flashcards
Total Work in Recursion
Total Work in Recursion
Signup and view all the flashcards
Big O notation
Big O notation
Signup and view all the flashcards
Complexity Analysis
Complexity Analysis
Signup and view all the flashcards
Recurrence Relation
Recurrence Relation
Signup and view all the flashcards
T(n)
T(n)
Signup and view all the flashcards
O(n)
O(n)
Signup and view all the flashcards
Inductive Proof
Inductive Proof
Signup and view all the flashcards
Inductive Hypothesis (IH)
Inductive Hypothesis (IH)
Signup and view all the flashcards
Constants c and d
Constants c and d
Signup and view all the flashcards
Tight Bound
Tight Bound
Signup and view all the flashcards
Total impact at layer
Total impact at layer
Signup and view all the flashcards
T(n) Recursion
T(n) Recursion
Signup and view all the flashcards
Base case T(1)
Base case T(1)
Signup and view all the flashcards
Layer count
Layer count
Signup and view all the flashcards
Node Impact
Node Impact
Signup and view all the flashcards
Depth of Recursion
Depth of Recursion
Signup and view all the flashcards
Total Cost T(n)
Total Cost T(n)
Signup and view all the flashcards
Logarithmic Cost
Logarithmic Cost
Signup and view all the flashcards
Polynomial Growth
Polynomial Growth
Signup and view all the flashcards
Study Notes
Algorithms and Data Structures
- Lecture topic: Recurrence Relations
- Lecture date: Winter Term 2024/25, 5th lecture
Solving Recurrence Relations
- Question: Does T(n) = 2 · T(n/2) + 4n (with T(1) = 0) imply T(n) ∈ O(nlogn)?
- Claim: There exists a c > 0 such that T(n) ≤ cn log₂ n.
- Proof: By induction over n.
- Base case: T(1) ≤ 0
- Inductive hypothesis: T(k) ≤ ck log₂ k holds for all k < n.
- Using the recurrence relation and the inductive hypothesis: T(n) = 2T(n/2) + 4n ≤ 2c (n/2) log₂(n/2) + 4n = 2 cn log₂ n - 2cn log₂ 2 + 4n = 2 cn log₂ n - 2cn + 4n
- For T(n) ≤ cn log₂ n, we need 2cn log₂ n − 2cn + 4n ≤ cn log₂ n
- The above inequality can be satisfied when c ≥ 4.
- Conclusion: Therefore, T(n) ∈ O(n log n) if c ≥ 4.
Another Example
- Recurrence Relation: T(n) = T([n/2]) + T([n/2]) + 1
- Claim: T(n) ∈ O(n)
- Proof: Induction over n.
- Hypothesis: T(k) ≤ ck for all k < n.
- Using the recurrence relation and inductive hypothesis: T(n) = T([n/2]) + T([n/2]) + 1 ≤ c[n/2] + c[n/2] + 1 = cn + 1
- Conclusion: This proves T(n)∈O(n)
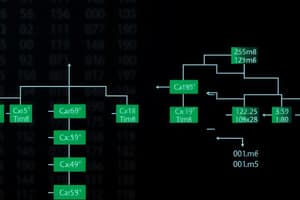
Recursion Tree Method
- Example: T(n) = 3T(n/4) + n²
- Analysis: The recursion tree method is used to analyze the time complexity of the recurrence relation. The table below gives an indication of the impact on different layers.
Layer Node count (Layer) Impact (Layer) 0 30 = 1 n2 1 31 = 3 3(n/4)2 i 3i (n/4)2 log4 n nlog4 3 - Conclusion: The recurrence is O(n2).
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.