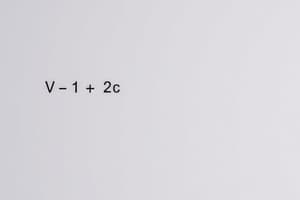Real Gas vs Ideal Gas

• An ideal gas, or perfect gas, is a hypothetical concept used in chemistry and physics to simplify the study of gases
• An ideal gas strictly obeys Boyle's Law (P∝1/V at constant T), Charles's Law (V∝T at constant P), and other classical gas laws under all conditions

Ideal Gas Equation

• PV=nRT, where:
  • P = Pressure of the gas
  • V = Volume of the gas
  • n = Number of moles of the gas
  • R = Universal gas constant
  • T = Temperature in Kelvin
• Real gases follow gas laws only approximately under certain conditions and deviate from ideal gas behavior, especially with changes in P and T
• Real gases obey gas laws reasonably well when pressure is low or temperature is high, minimizing intermolecular forces effects

Intermolecular forces of real gases

• Under conditions, intermolecular forces and finite size of gas particles are minimal in real gases, behaving similarly to an ideal gas
• No perfect or ideal gases exist in nature; All gases such as O2, N2, and CO2 are real gases
• As pressure increases, molecules of a real gas are forced closer together, leading to increased impact of intermolecular forces and deviation from gas law predictions
• As T decreases, the kinetic energy of gas decreases, intermolecular forces become more significant, causing further deviations from ideal behavior
• All gases are real, and their behavior depends on pressure and temperature conditions
• Models like the Van der Waals equation are used to predict gas behavior under various conditions

Deviation from ideal behavior

• According to Boyle's law, PV is constant when T is unchanged
• Plotting PV against P should yield a horizontal line, however real gases do not follow this exactly
• Instead of a straight line, two different curves are obtained due to intermolecular forces and the finite size of gas molecules
• At low pressure, gases approximate ideal behavior, but deviations become more pronounced as pressure increases or temperature decreases
• For gases like CO and CH4, PV first decreases then increases with pressure
• For gases like hydrogen and helium, PV continuously increases with pressure

Compressibility factor

• Temperature and pressure effects can be studied in terms of compressibility factor 'z', where z = 1 for an ideal gas at all temperatures and pressures
• For real gases, z varies with changes in temperature and pressure
• Plots of z vs. P at different constant temperatures for nitrogen gas show varying curves
• As temperature increases the minimums in the curves shift upwards until z nears 1 over an appreciable pressure range
• The Boyle temperature or Boyle point is the temperature at which a real gas behaves like an ideal gas over an appreciable pressure range
• Above the Boyle temperature, a gas shows positive deviations only

Boyle's Law Deviations

• These deviations can be observed using the compressibility factor (Z), where: Z = PV/nRT

Charles Gay-Lussac's Law

• The volume of a gas is directly proportional to its absolute temperature when the P is kept constant → V/T=CONSTANT
• V1/T1 = V2/T2

Volume expansion

• All gases should have the same coefficient of volume expansion, defined as the fractional increase in volume per degree Celsius rise, and is temperature dependent
• For every 1°C rise in temperature, the volume of a gas should increase by 1/127 of its volume at 0°C
• This relationship holds only at low P, while at high P, gases deviate significantly from Charles Gay-Lussac's law

Van der Waals Equation

• Understanding differences in gases helps refine gas laws for real-world applications, where corrections like the Van der Waals equation are used
• At low pressures, gas molecules are far apart, and intermolecular forces are minimal and gases follow Charles Gay-Lussac's law closely
• As pressure increases, molecules are forced closer, the gas may expand less than expected due to the intermolecular forces opposing the volume increase
• Charles Gay-Lussac's law is foundational for understanding the relationship between temperature and volume, but its assumptions are only valid at low pressures

Causes for Deviation of Real Gases

• Deviations occur because real gases do not behave ideally due to intermolecular forces and molecular size, which become more prominent as P increases
• Gas laws are derived from kinetic theory of gases based upon certain assumptions
• At high P or low T, two assumptions of kinetic theory of gases become invalid

Assumptions leading to deviation

• The volume occupied by gas molecules is negligible compared to the total volume of the gas
• The forces of attraction or repulsion between gas molecules are negligible

Conditions for valid assumptionss

• Assumptions are only valid if the pressure is low or the temp is high, so the distance between molecules is large
• If the pressure is high or the temperature is low, gas molecules get closer, invalidating these assumptions
• The forces of attraction or repulsion between the molecules are not negligible

Van der Waals Equation

• Johannes Diderik van der Waals made a breakthrough in understanding real gases in 1873
• The ideal gas law (PV=nRT) failed to describe gases accurately under high P and low T
• Real gases deviate from ideal behavior due to key factors: Intermolecular Forces and Finite Molecular Volume

Intermolecular forces

• Unlike ideal gases, real gas molecules attract each other, reducing the pressure exerted on container walls

Finite Molecular Volume

• Unlike point-like particles assumed in ideal gases, real gas molecules occupy space, reducing available volume for movement

Correction of Volume and Pressure

• Van der Waals obtained an equation for real gases by correcting for volume and pressure
• U is the actual volume occupied by one mole of gas molecules
• The effective volume occupied by gas molecules is actually four times the actual volume i.e., equal to 4 U
• Let it be represented by b. The volume b = co-volume or excluded volume.
• The free space for movement: (V- b).
• The gas molecule is attracted by all other gas molecules surrounding it
• For a molecule near the wall of the container, the molecules inside the gas exert some net inward pull on it
• The observed pressure is smaller than it would if there were no inward pull because it's "dragging back"
• Correction depends on: number of molecules surrounding a molecule, and the total number of molecules
• Each factor depends upon the density (ρ) of the gas

Van der Waals Equation

• The constants a and b are called van der Waals constants, and depend on gas nature, and independent of temperature and P
• For n moles of gas, the corrected pressure become P+an²/ V2 and the effective volume = V- nb
• Van der Waals equation takes the form: (P+an²/ V2) (V-nb) =nRT

Significance of Constants

• Values of "a" are greater for easily liquefiable gases than for so-called permanent gases
• The value of "a" increases with the ease of liquefaction, thus it measures intermolecular forces of attraction in a gas
• "b" is the "effective volume" of the gas molecules
• The constancy in the value of b confirms that gas molecules are incompressible across a range of temperaturs and pressures

Behavior of Real Gases

• At extremely low pressure V is very large
• The van der Waals equation reduces to PV = RT
• Gases obey the ideal gas equation

Moderate Pressure conditions

• As P increases, V decreases and a/V² increases
• The van der Waals equation reduces to PV = RT - a/V
• PV is less than RT by a factor of a/V
• As P increases, V decreases, so a/V increases
• PV decreases until a dip is obtained

High Pressure conditions

• V is so small such that b can no longer be neglected
• The van der Waals equation reduces to PV = RT + Pb
• PV is greater than RT by a factor of Pb
• As P is increased, the factor Pb increases, the product PV increases.
• At any P, if T is very high, the van der Waals equation reduces to PV = RT & the real gas behaves like an ideal gas

Exceptional Behavior of H and He

• For gases like hydrogen and helium, intermolecular forces of attraction are extremely small, so the van der Waals equation remains applicable
• The van der Waals equation is: P (V -b) = RT or PV = RT + Pb
• Hydrogen and helium show positive deviation only as the value of P increases

Kammerlingh-Onnes Virial Equation of State

• This is a thermodynamic model used to describe real gases, with a series expansion, and introduces a compressibility factor (Z) to calculate the power series
• PV= A + BP + CP2 + DP3 + or PV = RT ( 1 + BP + CP2 + DP3 + ...)
• The coefficients A, B, C etc., are first, second, third, etc., termed virial coefficients
• Points to note about the above equation:
  • The virial coefficients are different for different gases
  • At very low pressure, only the first virial coefficient is significant and equal to RT, i.e. A= RT
  • At higher pressures, other virial coefficients become more important
  • For any gas, values of A, B, C, are constant at constant temperature, but change with temperature
  • The first virial coefficient A is always positive and increases with temperature
• Boyle's temperature is the temperature at which a real gas most acts like an ideal gas over a range of pressures
• At the Boyle's temperature, the compressibility factor (Z for real gases) = 1 for a range of pressures, which means the effects of intermolecular forces is minimized

Equations of State

• Besides van der Waals equations and the virial equation, there exist a number of equations to study P-V-T relations
• One such equation is the Berthelot Equation, which is an empirical modification of the van der Waals equation of state

Dieterici Equation

• This is an empirical model similar to the van der Waals equation, incorporating intermolecular forces
• Satisfactory results at moderate pressure
• At higher pressures, the results has great agreement with experimental data
• The Redlich-Kwong is an improved model for describing real gases, refining the Van der Waals equation for better accuracy at higher temperatures and pressures
• The Clausius Equation studies the variance a with temperature, Clausius

Explore the behavior of real gases and their deviations from ideal gas laws. Understand conditions for ideal behavior, effects of pressure, and compressibility factors. Learn how Charles Gay-Lussac's Law applies.