Parabola: Direction of Opening Quiz

Questions and Answers

What indicates that a parabola opens upward?

The coefficient of x is negative.

The quadratic equation has a linear term.

The vertex is at the origin.

The coefficient a is greater than zero. (correct)

In a downward opening parabola, what is true about its vertex?

It represents the lowest point of the graph.

It has no intersection with the y-axis.

It is located at the origin (0,0).

It is the highest point of the graph. (correct)

Which equation represents a parabola that opens downward?

y = 0.5x^2 + 2

y = 2x^2 - 9

y = 3x^2 + 4

y = -5x^2 + 1 (correct)

What is the role of the coefficient 'a' in a quadratic equation of a parabola?

<p>It affects the width and direction of opening.</p> Signup and view all the answers

What is the axis of symmetry for a parabola represented by the vertex form equation y = a(x - h)^2 + k?

<p>x = h</p> Signup and view all the answers

Study Notes

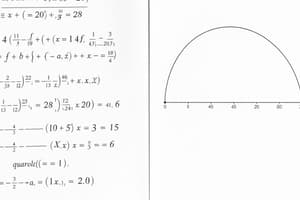
Parabola: Direction of Opening

Definition: A parabola is a symmetrical, U-shaped curve defined by a quadratic equation in the form (y = ax^2 + bx + c).
Direction of Opening:
- Upward Opening:
  - Occurs when the coefficient (a > 0).
  - Vertex is the lowest point.
  - Example: (y = 2x^2 + 3).
- Downward Opening:
  - Occurs when the coefficient (a < 0).
  - Vertex is the highest point.
  - Example: (y = -2x^2 + 3).
Vertex:
- The highest or lowest point of the parabola.
- Located at the point ((h, k)) for the vertex form (y = a(x - h)^2 + k).
Axis of Symmetry:
- A vertical line that passes through the vertex.
- Given by the equation (x = h).
Applications:
- Used in physics (projectile motion), engineering (design of satellite dishes), and economics (profit maximization).
Graphing:
- Identify direction of opening based on (a).
- Locate vertex and axis of symmetry.
- Plot additional points for accuracy.

Parabola Overview

A parabola is a U-shaped curve that is symmetrical and defined by the quadratic equation format (y = ax^2 + bx + c).

Direction of Opening

Upward Opening:
- Occurs when the coefficient (a) is greater than zero ((a > 0)).
- The vertex serves as the lowest point of the parabola.
- Example equation: (y = 2x^2 + 3).
Downward Opening:
- Occurs when the coefficient (a) is less than zero ((a < 0)).
- The vertex acts as the highest point of the parabola.
- Example equation: (y = -2x^2 + 3).

Vertex

The vertex represents the pivotal point, either the highest or lowest on the parabola.
In vertex form (y = a(x - h)^2 + k), the vertex is located at ((h, k)).

Axis of Symmetry

The axis of symmetry is a vertical line that bisects the parabola through its vertex.
It is represented by the equation (x = h), where (h) is the x-value of the vertex.

Applications

Parabolas are utilized in various fields:
- Physics: For modeling projectile motion.
- Engineering: In the design of satellite dishes.
- Economics: To demonstrate profit maximization techniques.

Graphing Techniques

To graph a parabola:
- Determine the direction of opening by examining the coefficient (a).
- Find the vertex and draw the axis of symmetry.
- Plot additional points to ensure the graph's accuracy and shape.

Description

Test your understanding of parabolas with this quiz focused on the direction of opening. Learn to identify whether a parabola opens upward or downward based on its quadratic equation. Explore concepts such as the vertex, axis of symmetry, and applications in various fields.