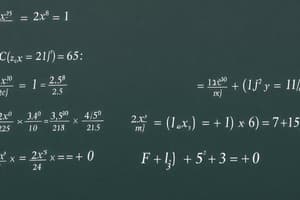Podcast
Questions and Answers
What is the primary focus of the module indicated in the content?
What is the primary focus of the module indicated in the content?
In which educational level is the module targeted?
In which educational level is the module targeted?
What method is highlighted in this module for solving quadratic equations?
What method is highlighted in this module for solving quadratic equations?
Who is listed as the Secretary of Education in the module's details?
Who is listed as the Secretary of Education in the module's details?
Signup and view all the answers
What is the significance of Republic Act 8293 mentioned in the content?
What is the significance of Republic Act 8293 mentioned in the content?
Signup and view all the answers
What is the value of $−√49$?
What is the value of $−√49$?
Signup and view all the answers
If $x^2 = 225$, what are the possible values of x?
If $x^2 = 225$, what are the possible values of x?
Signup and view all the answers
What is the solution to the equation $x^2 + 6 = 6$?
What is the solution to the equation $x^2 + 6 = 6$?
Signup and view all the answers
If the area of a square is $s^2 = 1,764$ sq.units, what is the value of s?
If the area of a square is $s^2 = 1,764$ sq.units, what is the value of s?
Signup and view all the answers
What is the value of $√400$?
What is the value of $√400$?
Signup and view all the answers
Study Notes
Solving Quadratic Equations by Extracting Square Roots
- Quadratic equations can be solved using the square root method when presented in the form ( x^2 = c ).
- If ( x^2 = c ), the solutions are ( x = \sqrt{c} ) or ( x = -\sqrt{c} ).
- For quadratic equations with one solution, set ( c ) to a non-negative value.
Examples of Solving Quadratic Equations
-
Example 1: Solving ( x^2 = 64 )
- Extract square root: ( x = \pm 8 )
- Solutions are ( 8 ) and ( -8 ).
-
Example 2: Solving ( x^2 + 6 = 6 )
- Rearrange to ( x^2 = 0 ).
- Take square roots: ( x = 0 ).
- Solution is ( 0 ).
-
Example 3: Solving ( 9x^2 + 16 = 0 )
- Rearrange to ( 9x^2 = -16 ), showing no real solutions (as square roots of negative numbers are imaginary).
-
Example 4: Solving ( 2(x + 4)^2 = 18 )
- Divide by 2 to get ( (x + 4)^2 = 9 ).
- The square roots yield equations ( x + 4 = 3 ) or ( x + 4 = -3 ).
- Solutions are ( x = -1 ) and ( x = -7 ).
Steps for Extracting Square Roots
- Write the equation in the form ( x^2 = \frac{c}{a} ).
- Extract square roots from both sides, adding a ± sign before the square root.
- Solve the resulting equations and verify the solutions through substitution.
Key Definitions
- Square Root Property: States that if ( x^2 = c ), then ( x = \sqrt{c} ) or ( x = -\sqrt{c} ).
- An equation with ( c < 0 ) yields no real solutions, and the solutions are imaginary.
Practice Problems
- Solve quadratic equations such as ( x^2 - 49 = 0 ), ( 9x^2 - 25 = 0 ), ( 4x^2 + 1 = 5 ) by extracting square roots.
- Check solutions through substitution.
Assessment Questions
- Identify the correct property related to quadratic equations, solutions of specific values, and practical methods for solving quadratic equations.
- Determine the roots and simplify expressions involving square roots.
Important Notes
- Quadratic equations can have two solutions (real), one solution (real), or no solutions (imaginary).
- Practice multiple problems to gain proficiency in this method of solving quadratic equations.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Related Documents
Description
This quiz focuses on solving quadratic equations by extracting square roots, tailored for Grade 9 Mathematics. It covers the core concepts outlined in Quarter 1, Module 2. Enhance your understanding and mastery of these essential mathematical principles.
