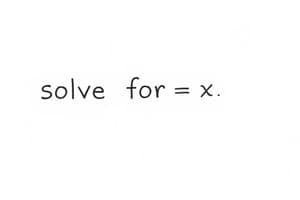Podcast
Play an AI-generated podcast conversation about this lesson
Questions and Answers
Isolate the variable 's' in the equation P = 4s.
Isolate the variable 's' in the equation P = 4s.
s = \frac{P}{4}
Isolate the variable 't' in the equation ( v = \frac{d}{t} ).
Isolate the variable 't' in the equation ( v = \frac{d}{t} ).
t = \frac{d}{v}
Isolate the variable 'y' in the equation 4x + 2y = 6.
Isolate the variable 'y' in the equation 4x + 2y = 6.
y = \frac{6 - 4x}{2}
Isolate the variable 'v' in the equation ( t = \frac{\sqrt{v^2-u^2}}{30} ).
Isolate the variable 'v' in the equation ( t = \frac{\sqrt{v^2-u^2}}{30} ).
Signup and view all the answers
Isolate the variable 't' in the equation ( S = \frac{(u+v)}{2} t ).
Isolate the variable 't' in the equation ( S = \frac{(u+v)}{2} t ).
Signup and view all the answers
Flashcards are hidden until you start studying
Study Notes
Isolate Variables
- To isolate a variable, you want to manipulate the equation to get your desired variable on one side by itself and everything else on the other side.
- This involves using inverse operations until the variable is by itself.
Isolate s
- P = 4s
- Divide both sides by 4
- Therefore s = P/4
Isolate t
- $v = \frac{d}{t}$
- **Multiply both sides by 't' **
- Divide both sides by 'v'
- Therefore t = d/v
Isolate y
- 4x + 2y = 6
- Subtract 4x from both sides
- **Divide both sides by 2 **
- Therefore y = (6 - 4x)/2
Isolate v
- $t = \frac{\sqrt{v^2-u^2}}{30}$
- Multiply both sides by 30
- Square both sides
- Add u² to both sides
- Take the square root of both sides
- Therefore v = √( (30t)² + u² )
Isolate t
- **$S = \frac{(u+v)}{2}$ t **
- Multiply both sides by 2
- Divide both sides by (u+v)
- Therefore t = 2S / (u+v)
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
