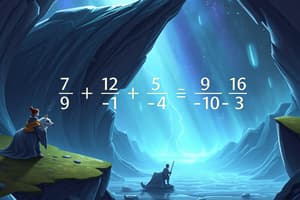Fraction Operations Quiz

Study Notes

Fraction operations involve manipulating different parts of fractions depending on what you want to do with them — whether it's adding, subtracting, multiplying, or dividing. Here we delve into each operation one by one, while considering how to handle improper fractions along the way.

Adding Fractions

To add two fractions together, they must have a common denominator. If they don’t already share this common part, change them so they both do, like this: [\frac{3}{5} + \frac{8}{5}], which equals (\frac{11}{5}). To find a common multiple, look for a number that evenly divides both denominators. For example, if your original fractions were (\frac{7}{19} + \frac{16}{49}), making (49) their lowest common denominator would work.

Subtracting Fractions

Subtraction is similar to addition except the signs flip over — instead of (+), you get (-); instead of (=), you get (=). So, for instance, if you started with (\frac{11}{8}-\frac{3}{8}=\frac{8}{8}=1), that means there was enough room left after taking away (\frac{3}{8}) from (\frac{11}{8}) to fill up another whole thing.

Multiplying Fractions

When multiplying fractions, take the product of their numerators and put it over the product of their denominators. This gives you a new fraction with a larger decimal value. For example, when you multiply (\frac{3}{8}\times\frac{4}{3}), you end up with (\frac{12}{24}=\frac{1}{2}).

Dividing Fractions

You separate any factors in the denominator out of your division problem first, turning it into multiplication. Then multiply top and bottom by whatever you separated out of the denominator. For instance, say you want to divide (\frac{8}{3}) by (\frac{1}{2}), you could rewrite (\frac{1}{2}) as (\frac{2}{4}) and then turn the division problem into a multiplication problem: (\frac{8}{3}\times\frac{2}{4}). This simplifies to (\frac{16}{12}=\frac{4}{3}).

Converting Improper Fractions to Mixed Numbers

An improper fraction has a numerator bigger than its denominator. It can always be converted to a mixed number because it represents more than one unit. Simply move the decimal point of the numerator one place to the right. In other words, the quotient of an integer divided by another nonzero integer will result in either a fraction ((<!1)) or a whole number plus a fraction ((\geq!1)).

For example, the fraction (\frac{15}{4}) is equivalent to (3\frac{1}{4}). That means you can think of it as three units and four fourths. Another example is (\frac{7}{4}), which is equal to (1\frac{3}{4}): One unit plus three fourths.

Description

Test your knowledge on adding, subtracting, multiplying, dividing fractions, and converting improper fractions to mixed numbers. Learn how to handle common denominators, manipulate numerators and denominators, and simplify fractions effectively.