Finite Difference Method for PDEs

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the finite difference method (FDM)?

The finite difference method is a numeric approximation technique used to solve PDEs by discretizing the problem into a system of algebraic equations.

Name one advantage of using the finite difference method (FDM) for solving PDEs.

Simplicity

What type of problems can the finite difference method (FDM) be applied to?

A wide range of PDE problems, including linear and nonlinear equations

What does the accuracy of the finite difference method (FDM) depend on?

The size of the grid and the choice of time step Signup and view all the answers

Give an example of a PDE problem to which the finite difference method (FDM) has been applied.

Elliptic Equations Signup and view all the answers

What fields benefit from the numerical solution of PDEs using methods like the finite difference method?

Finance, economics, and engineering Signup and view all the answers

What are some applications of the Du Fort and Frankel finite difference scheme?

Option pricing, asset valuation, multi-variable cell population balance models Signup and view all the answers

What challenges and potential future directions are associated with the finite difference method?

Stability, error estimation, computational efficiency Signup and view all the answers

What is crucial for obtaining accurate and reliable solutions when using finite difference schemes?

Stability Signup and view all the answers

What aspect of using FDM is important in terms of error estimation?

Estimating the error due to the finite boundary Signup and view all the answers

What becomes prohibitive as the size of the grid and the number of time steps increase?

The computational cost of FDM Signup and view all the answers

What have researchers developed for estimating the stability of finite difference schemes?

Various criteria such as stability estimates, coercivity, and almost coercivity inequalities Signup and view all the answers

For what type of problems have finite difference algorithms been developed?

Multi-variable cell population balance models Signup and view all the answers

What have researchers developed for providing increasingly accurate approximations and error estimates for various cases?

Sequences of boundary conditions Signup and view all the answers

What are some potential areas for future research related to the finite difference method?

Stability, error estimation, computational efficiency Signup and view all the answers

What are the main characteristics that make the finite difference method an attractive choice for researchers and practitioners?

Simplicity, accuracy, wide applicability Signup and view all the answers

Study Notes

Numerical Solution of PDEs: Finite Difference Methods

The numerical solution of partial differential equations (PDEs) is a crucial aspect of various fields, including finance, economics, and engineering. One of the most common numerical methods for solving PDEs is the finite difference method (FDM). This article will discuss the finite difference method and its applications in solving PDEs.

Finite Difference Method

The finite difference method is a numeric approximation technique used to solve PDEs. It involves discretizing the problem into a system of algebraic equations by replacing continuous operations with finite differences. There are several advantages of using the FDM, including:

Simplicity: The method is relatively simple to implement and can be easily adapted to various problems.
Accuracy: FDM can provide accurate solutions to PDEs, with the accuracy depending on the size of the grid and the choice of time step.
Wide applicability: The method can be applied to a wide range of PDE problems, including linear and nonlinear equations.

Applications of Finite Difference Method in PDEs

The finite difference method has been applied to various PDE problems, including:

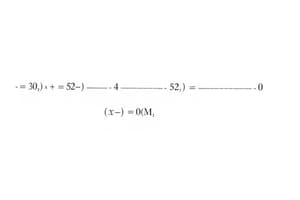
Elliptic Equations: FDM has been used to solve elliptic boundary value problems, such as the Laplace equation and its variational formulation. The method has been shown to provide improved convergence rates with no additional computational work.
Financial Problems: The Du Fort and Frankel finite difference scheme has been applied to a class of financial problems, such as option pricing and asset valuation. The method has been shown to provide accurate and stable solutions to these problems.
Multi-Variable Cell Population Balance Models: Finite difference algorithms have been developed for the solution of multi-variable cell population balance models, which are used in various fields, including biology and chemistry. These algorithms have been shown to provide accurate and efficient solutions to these complex problems.

Challenges and Future Directions

Despite its widespread application, the finite difference method also has some challenges and areas for future research. Some of these challenges and potential future directions include:

Stability: Ensuring the stability of finite difference schemes is crucial for obtaining accurate and reliable solutions. Researchers have developed various criteria for estimating the stability of these schemes, such as stability estimates, coercivity, and almost coercivity inequalities.
Error Estimation: Estimating the error due to the finite boundary is an important aspect of using FDM. Researchers have developed sequences of boundary conditions that provide increasingly accurate approximations, along with error estimates for various cases.
Computational Efficiency: As the size of the grid and the number of time steps increase, the computational cost of FDM can become prohibitive. Researchers are exploring more efficient computational methods and techniques to improve the performance of FDM in solving large-scale PDE problems.

In conclusion, the finite difference method is a powerful and versatile tool for solving a wide range of PDE problems. Its simplicity, accuracy, and wide applicability make it an attractive choice for researchers and practitioners in various fields. However, challenges such as stability, error estimation, and computational efficiency must be addressed to further improve the effectiveness of FDM in solving PDEs.

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Description

Explore the finite difference method (FDM), a numerical approximation technique used to solve partial differential equations (PDEs). Learn about its applications in various fields such as finance, engineering, and biology, along with challenges and future directions for improvement.