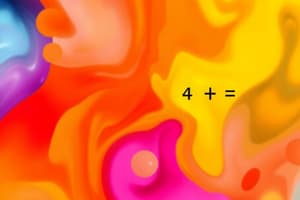Podcast
Questions and Answers
Mapping from the sample space to the real line is a characteristic of what?
Mapping from the sample space to the real line is a characteristic of what?
- Descriptive statistics
- A random variable (correct)
- Inferential statistics
- A continuous function
Which of the following is NOT a key feature of a discrete random variable?
Which of the following is NOT a key feature of a discrete random variable?
- Has a countable number of distinct values.
- Has a finite number of distinct values.
- Values are on a subset of the real line.
- Can take on any value within a given range. (correct)
What does the probability mass function (PMF) of a random variable X represent?
What does the probability mass function (PMF) of a random variable X represent?
- The probability that X is less than or equal to a certain value.
- The probability that X is greater than a certain value.
- The probability that X is equal to a specific value. (correct)
- The average value of X.
If a random variable X can only take two values, 0 and 1, what type of random variable is it?
If a random variable X can only take two values, 0 and 1, what type of random variable is it?
An indicator random variable X is defined as X=1 if event A occurs and X=0 otherwise. What must be true about events A and its complement?
An indicator random variable X is defined as X=1 if event A occurs and X=0 otherwise. What must be true about events A and its complement?
With a single throw of a fair six-sided die, what is the probability of getting a number greater than 4 according to its Probability Mass Function?
With a single throw of a fair six-sided die, what is the probability of getting a number greater than 4 according to its Probability Mass Function?
What is a key property of a Cumulative Distribution Function?
What is a key property of a Cumulative Distribution Function?
What does the expectation of a random variable represent?
What does the expectation of a random variable represent?
How is the expected value of a discrete random variable calculated?
How is the expected value of a discrete random variable calculated?
For a Bernoulli random variable, if 'p' represents the probability of success, what is its expected value?
For a Bernoulli random variable, if 'p' represents the probability of success, what is its expected value?
An insurance company models payouts for a natural disaster. They estimate the following probabilities: No disaster (probability 0.6, payout 0), Storm (probability 0.3, payout 600 pesos), Storm and Flood (probability 0.1, payout 1000 pesos). What is the expected payout?
An insurance company models payouts for a natural disaster. They estimate the following probabilities: No disaster (probability 0.6, payout 0), Storm (probability 0.3, payout 600 pesos), Storm and Flood (probability 0.1, payout 1000 pesos). What is the expected payout?
What does the variance of a random variable measure?
What does the variance of a random variable measure?
How can the variance of a random variable X be computed?
How can the variance of a random variable X be computed?
What is the variance of a Bernoulli distribution with success probability 'p'?
What is the variance of a Bernoulli distribution with success probability 'p'?
Which of the following is the MOST direct application of a random variable?
Which of the following is the MOST direct application of a random variable?
In the context of random variables, what does 'countable' refer to when describing the number of distinct values?
In the context of random variables, what does 'countable' refer to when describing the number of distinct values?
Why is assigning numbers to elements in the Sample Space S necessary for statistical analysis?
Why is assigning numbers to elements in the Sample Space S necessary for statistical analysis?
Given the PMF for a fair six-sided die, what is the probability of rolling an even number?
Given the PMF for a fair six-sided die, what is the probability of rolling an even number?
Which of the following is the characteristic of the Cumulative Distribution Function (CDF)?
Which of the following is the characteristic of the Cumulative Distribution Function (CDF)?
Which of the following statements best describes the role of expectation in decision-making under uncertainty?
Which of the following statements best describes the role of expectation in decision-making under uncertainty?
A random variable X is defined such that X = 1 with probability p and X = 0 with probability 1-p. What is $E[X^2]$?
A random variable X is defined such that X = 1 with probability p and X = 0 with probability 1-p. What is $E[X^2]$?
How does climate change potentially destabilize the Insurance Industry, according to the information provided?
How does climate change potentially destabilize the Insurance Industry, according to the information provided?
A life insurance company wants to model the economic risks of a certain disease. Why would they use a random variable to model this?
A life insurance company wants to model the economic risks of a certain disease. Why would they use a random variable to model this?
What key challenge do climate change and natural disasters pose to the insurance industry, as hinted by the insurance problem example?
What key challenge do climate change and natural disasters pose to the insurance industry, as hinted by the insurance problem example?
If for every 1000 pesos of insured property, damaged inventories result in a payout of 600 pesos for a storm and 1000 pesos for a combined storm and flood, what does this describe in the context of insurance modeling?
If for every 1000 pesos of insured property, damaged inventories result in a payout of 600 pesos for a storm and 1000 pesos for a combined storm and flood, what does this describe in the context of insurance modeling?
What does the assumption "climate change does not worsen" imply for the insurance problem?
What does the assumption "climate change does not worsen" imply for the insurance problem?
In the context of an insurance payout as a random variable, what does a higher payout variance suggests to the insurance company?
In the context of an insurance payout as a random variable, what does a higher payout variance suggests to the insurance company?
Consider a simplified probability model where an insurance company in the Philippines distinguishes three events on a yearly basis: no natural disaster, a storm and a storm and flood. If they want to estimate their potential yearly losses, which tool should they use?
Consider a simplified probability model where an insurance company in the Philippines distinguishes three events on a yearly basis: no natural disaster, a storm and a storm and flood. If they want to estimate their potential yearly losses, which tool should they use?
Which of the following real-world phenomena can NOT be appropriately modeled by a random variable?
Which of the following real-world phenomena can NOT be appropriately modeled by a random variable?
Wage (W) and Education (E) are discrete random variables. Given that $P(W=High, E=College) = 0.19$, $P(W=High, E=Not College) = 0.12$, $P(W=Low, E=College) = 0.17$ and $P(W=Low, E= Not College) = 0.52$, what is the probability of having a high wage?
Wage (W) and Education (E) are discrete random variables. Given that $P(W=High, E=College) = 0.19$, $P(W=High, E=Not College) = 0.12$, $P(W=Low, E=College) = 0.17$ and $P(W=Low, E= Not College) = 0.52$, what is the probability of having a high wage?
Wage (W) and Education (E) are discrete random variables. Given that $P(W=High, E=College) = 0.19$, $P(W=High, E=Not College) = 0.12$, $P(W=Low, E=College) = 0.17$ and $P(W=Low, E= Not College) = 0.52$, what is the probability of having a college education?
Wage (W) and Education (E) are discrete random variables. Given that $P(W=High, E=College) = 0.19$, $P(W=High, E=Not College) = 0.12$, $P(W=Low, E=College) = 0.17$ and $P(W=Low, E= Not College) = 0.52$, what is the probability of having a college education?
To calculate Variance in an insurance problem, what must the company first estimate?
To calculate Variance in an insurance problem, what must the company first estimate?
Suppose $f(x) = 1/3$, for $x = -1, 0, 1$, what is $E[x]$?
Suppose $f(x) = 1/3$, for $x = -1, 0, 1$, what is $E[x]$?
Suppose $f(x) = 1/3$, for $x = -1, 0, 1$, what is the variance?
Suppose $f(x) = 1/3$, for $x = -1, 0, 1$, what is the variance?
An economist is modeling the annual income of individuals in a city. He decides to use a random variable. What is the most important assumption he is making?
An economist is modeling the annual income of individuals in a city. He decides to use a random variable. What is the most important assumption he is making?
Why is statistical analysis difficult to use with climate change disasters and insurance?
Why is statistical analysis difficult to use with climate change disasters and insurance?
In probability, why is a random sample important?
In probability, why is a random sample important?
Flashcards
What is a random variable?
What is a random variable?
Mapping from the sample space to the real line.
What is a discrete random variable?
What is a discrete random variable?
A random variable which takes only discrete values.
What is Probability Mass Function (PMF)?
What is Probability Mass Function (PMF)?
The probability that a discrete random variable X takes a specific value.
What is a Bernoulli Random Variable?
What is a Bernoulli Random Variable?
Signup and view all the flashcards
What happens if X(success)=1?
What happens if X(success)=1?
Signup and view all the flashcards
What happens if X(failure)=0?
What happens if X(failure)=0?
Signup and view all the flashcards
What is an Indicator Random Variable?
What is an Indicator Random Variable?
Signup and view all the flashcards
What is the Expectation of a Random Variable?
What is the Expectation of a Random Variable?
Signup and view all the flashcards
What happens if X=1 with probability p?
What happens if X=1 with probability p?
Signup and view all the flashcards
What happens if X=0 with probability 1-p?
What happens if X=0 with probability 1-p?
Signup and view all the flashcards
Climate and the Insurance Industry?
Climate and the Insurance Industry?
Signup and view all the flashcards
Study Notes
- Probability, Statistics and Econometrics Econ 10003
- Random Variables - 2025
Random Variables
- Mapping from the sample space to the real line
- Used in games of chance, like coin tosses or single dice throws
- Assigns a number corresponding to an element in the Sample Space S
- Forms the basis for statistical analysis
- Following a single flip of a coin, a random variable X can be defined
- The values X will take before the coin flip are unknown
Discrete Random Variable
- Discrete: X only takes values on a subset of the real line
- Countable number of distinct values; finite number of distinct values
- Probability mass function (PMF) of a random variable X.
- PMF notations include f
- Example:
- X = 1, P(X=x) = 0.5 (from a single coin toss)
- X = 0, P(X=x) = 0.5 (from a single coin toss)
Joint Probabilities
- Wage and Education
- H = High Wage
- L = Low Wage
- C = College
- N = No College
- Education E, P(E=e)
- C = 1 = 0.36
- N = 0 = 0.64
- Wage W, P(W=w)
- H = 1 = 0.31
- L = 0 = 0.69
Wages earners in US (2009)
- The distribution of wages in the US in 2009
- W = 1 = 0.3
- W = 0 = 0.7
College attendance in the US (2009)
- The distribution of college attendance in the US in 2009
- C = 1 = 0.36
- C = 0 = 0.64
Bernoulli Random Variable
- Random variable X has only two possible values: 0 and 1
- X(success) = 1 in a random experiment
- X(failure) = 0 in a random experiment
- P(X=1)=p
- P(X=0)=1-p
- The PMF of X can be written as
Indicator Random Variable
- Random variable X has only two possible values which are mutually exclusive and exhaustive
- X=1 if A occurs (e.g. an individual is a high wage earner)
- X=0 otherwise (e.g. an individual is a low wage earner)
- P(X=1)=p
- P(X=0)=1-p
Probability Mass Function
- The PMF for years of education in US (gathered from US data)
- X = Years of Education (US Wage Earners in 2009)
- 8 = 0.027
- 9 = 0.011
- 10 = 0.011
- 11 = 0.026
- 12 = 0.274
- 13 = 0.182
- 14 = 0.111
- 16 = 0.229
- 18 = 0.092
- 20 = 0.037
- X = Years of Education (US Wage Earners in 2009)
Probability Mass Function
- PMF from a single throw of a dice is 1/6
Cumulative Distribution Function
- Cumulative Distribution Function plot
- Cumulative Distribution Function properties
- Increasing
- Right continuous
- Cumulative Distribution Function (Find probabilities for intervals)
Expectation of a random variable
- Measure of central tendency
- Denoted as E(X)
- Average value with probability-weighted averaging
- Expected value, average or mean of the distribution
- Where denotes the PMF
Expectation of a Random Variable
- X=1 with probability p and X=0 with probability 1-p which yields and expected value
- For a Bernoulli random variable, same as the probability of a success
- Examples include the US wage, college attendance
- The average number of years of education is about 14
Insurance Problem
- Climate change is Destabilizing Insurance Industry, scientific American in 2003
- Every year 26 million people are pushed into poverty by natural disasters (The World Bank, 2017)
- Every year disasters cause an average $300 billion in economic losses (The World Bank, 2017)
Applications of Expectation
- An insurance company based in the Philippines decided to use a simplified probability model to describe the risks of natural disasters due to climate change
- Yearly Basis:
- No natural disaster with a probability of 0.6
- A storm disaster occurring with a probability of 0.3
- A combination of storm and flood disaster occurring with a probability of 0.1
- For every 1000 pesos of insured property, damaged inventories of recent years tell the following
- Payout is 600 pesos for a storm
- Payout is 1000 pesos for a combined storm and flood
- Zero payout when no disaster happens
- X is a random variable that represents the payout
- There is a likelihood of a storm occurring in 30% of the years, combined storm and flood in 10% of the years and no disaster in 60% of the years
- Assuming climate change does not worsen, and property insurance has a long duration
- The average yearly payout
Variance
- Variance of X
- Insurance problem
- Standard deviation
- Variance of X: can be computed as
- Let X be a random variable with the PMF, computing the mean and variance
- Let Y be a random variable with the PMF g, computing the mean and variance
Variance of a Bernoulli Distribution
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.