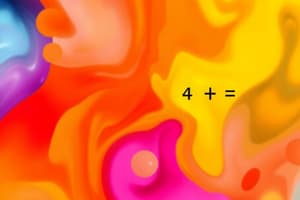Podcast
Questions and Answers
Which of the following is a characteristic of a discrete random variable?
Which of the following is a characteristic of a discrete random variable?
- Countable (correct)
- Consisting of real numbers
- Measurable within a range
- Taking any value within a given interval
Which of the following illustrates a continuous random variable?
Which of the following illustrates a continuous random variable?
- The number of cars that pass through an intersection in an hour.
- The number of heads when flipping a coin five times.
- The number of defective items in a production run.
- The height of students in a class. (correct)
What is a key property of a probability mass function (PMF)?
What is a key property of a probability mass function (PMF)?
- The probabilities sum up to any positive number.
- It can only be represented graphically.
- The probability of each value is between 0 and 1, inclusive, and the sum of all probabilities is 1. (correct)
- Each probability value is between -1 and 1.
In a probability distribution, what does P(X=x) represent?
In a probability distribution, what does P(X=x) represent?
When is the expected value of a discrete random variable equal to zero:
When is the expected value of a discrete random variable equal to zero:
Increasing the variance of a discrete random variable, while keeping the mean constant, indicates what?
Increasing the variance of a discrete random variable, while keeping the mean constant, indicates what?
How does the standard deviation relate to the variance of a discrete random variable?
How does the standard deviation relate to the variance of a discrete random variable?
Which expression represents the formula for the expected value, E(X), of a discrete random variable X, where $x_i$ are the values and $P(x_i)$ are their corresponding probabilities?
Which expression represents the formula for the expected value, E(X), of a discrete random variable X, where $x_i$ are the values and $P(x_i)$ are their corresponding probabilities?
Which of the following scenarios best illustrates a discrete random variable?
Which of the following scenarios best illustrates a discrete random variable?
In probability, what does 'sample space' refer to?
In probability, what does 'sample space' refer to?
A game involves rolling a fair six-sided die. If you roll a 1, you win $10; if you roll a 2 or 3, you win $5; otherwise, you lose. What is the expected value of playing this game?
A game involves rolling a fair six-sided die. If you roll a 1, you win $10; if you roll a 2 or 3, you win $5; otherwise, you lose. What is the expected value of playing this game?
What distinguishes a random variable from other types of variables?
What distinguishes a random variable from other types of variables?
What condition must be met for a function to be a valid probability mass function (PMF)?
What condition must be met for a function to be a valid probability mass function (PMF)?
Which of the following is NOT a direct characteristic of a discrete probability distribution?
Which of the following is NOT a direct characteristic of a discrete probability distribution?
A random variable X represents the number of heads in three coin flips. Which set represents all possible values of X?
A random variable X represents the number of heads in three coin flips. Which set represents all possible values of X?
A company models customer satisfaction on a scale of 1 to 5, with 5 being the most satisfied. If the distribution is discrete, what does it imply about customer satisfaction scores?
A company models customer satisfaction on a scale of 1 to 5, with 5 being the most satisfied. If the distribution is discrete, what does it imply about customer satisfaction scores?
In a game where the probability of winning is 1/4 and the payout is $20, what is the expected value of playing the game, assuming it costs $2 to play?
In a game where the probability of winning is 1/4 and the payout is $20, what is the expected value of playing the game, assuming it costs $2 to play?
What is the primary use of the variance of a discrete random variable?
What is the primary use of the variance of a discrete random variable?
Given two discrete random variables, X and Y, with the same expected value, what conclusion can be drawn if the variance of X is greater than the variance of Y?
Given two discrete random variables, X and Y, with the same expected value, what conclusion can be drawn if the variance of X is greater than the variance of Y?
Which of the following statements is true regarding continuous random variables?
Which of the following statements is true regarding continuous random variables?
What is the main difference between a discrete and continuous random variable?
What is the main difference between a discrete and continuous random variable?
If you have a discrete random variable with equally likely outcomes, how do you compute its expected value?
If you have a discrete random variable with equally likely outcomes, how do you compute its expected value?
What does an event with a probability of 0 indicate?
What does an event with a probability of 0 indicate?
What variable type is the number of pages in a book?
What variable type is the number of pages in a book?
What variable type is atmospheric temperature?
What variable type is atmospheric temperature?
If you play a game with a negative expectation, what does this most likely mean?
If you play a game with a negative expectation, what does this most likely mean?
Which of the following is required to calculate the probability mass function?
Which of the following is required to calculate the probability mass function?
A random variable X is defined as the sum of two six-sided dice. What is the probability of X=1?
A random variable X is defined as the sum of two six-sided dice. What is the probability of X=1?
A football team plays three consecutive games. If W represents a win and L a loss, what is the sample space?
A football team plays three consecutive games. If W represents a win and L a loss, what is the sample space?
In the context of a probability distribution, what does 'expected value' represent?
In the context of a probability distribution, what does 'expected value' represent?
If $X$ is a discrete random variable, which of the following is always true about its variance, denoted as $Var(X)$?
If $X$ is a discrete random variable, which of the following is always true about its variance, denoted as $Var(X)$?
A discrete random variable has possible values 1, 2, and 3 with probabilities 0.2, 0.5, and 0.3, respectively. What is the expected value of this random variable?
A discrete random variable has possible values 1, 2, and 3 with probabilities 0.2, 0.5, and 0.3, respectively. What is the expected value of this random variable?
In a binomial distribution, what does 'n' represent?
In a binomial distribution, what does 'n' represent?
In the formula for the Binomial distribution, what is C(n, r)?
In the formula for the Binomial distribution, what is C(n, r)?
What kind of values are restricted with Poisson Distribution?
What kind of values are restricted with Poisson Distribution?
Which scenario meets the requirement to use poisson distribution?
Which scenario meets the requirement to use poisson distribution?
In Poisson distribution, what does '' denote?
In Poisson distribution, what does '' denote?
Which statement is INCORRECT about the Poisson distribution?
Which statement is INCORRECT about the Poisson distribution?
At a call center the average number of support requests per 1 minute is 7. What would expression calculate 4 requests in the next minute? (Where e is Euler's number)
At a call center the average number of support requests per 1 minute is 7. What would expression calculate 4 requests in the next minute? (Where e is Euler's number)
At a sandwich shop the average number of the clients is 10 per 30 minutes. What is the probability of serving zero clients in that time? (Where e is Euler's number)
At a sandwich shop the average number of the clients is 10 per 30 minutes. What is the probability of serving zero clients in that time? (Where e is Euler's number)
Flashcards
What are Random Variables?
What are Random Variables?
Variables whose possible values are the numerical outcomes of a random experiment.
What is a Discrete Random Variable?
What is a Discrete Random Variable?
A random variable that can only take on a finite number of values, typically whole numbers.
What is a Continuous Random Variable?
What is a Continuous Random Variable?
A random variable that can take any value within a given range or interval (measureable).
What is Probability Mass Function?
What is Probability Mass Function?
Signup and view all the flashcards
What is a Probability Distribution Function?
What is a Probability Distribution Function?
Signup and view all the flashcards
Expected Value (Mean)
Expected Value (Mean)
Signup and view all the flashcards
What is Variance?
What is Variance?
Signup and view all the flashcards
Standard Deviation
Standard Deviation
Signup and view all the flashcards
What is Binomial Distribution?
What is Binomial Distribution?
Signup and view all the flashcards
Binomial Probability
Binomial Probability
Signup and view all the flashcards
What is Poisson Distribution?
What is Poisson Distribution?
Signup and view all the flashcards
Study Notes
- This document covers statistical analysis with software applications, focusing on discrete probability distributions, random variables, expected value, and variance.
- Rocelle Ann G. Terco is the facilitator for course AE 09 (Lec).
Learning Objectives
- Illustrate random variables, distinguishing between discrete and continuous types.
- Determine possible values for random variables.
- Illustrate probability distributions.
- Construct probability mass functions.
- Compute probabilities.
Flow of Session
- Review fundamental concepts.
- Receive an overview of the topic.
- Study examples of random variables using probability distributions.
- Learn about expected value and variance.
- Complete a checkpoint exercise.
Discrete Probability Distribution
- Chapter V focuses on discrete probability distributions.
- Random variables, which have properties and types, may be described by a probability distribution.
- Types of probability distribution include discrete and continuous, with discrete distributions having probability mass functions.
Random Variables
- Random variables represent variables whose possible values are numerical outcomes of a random experiment.
Types of Random Variables
- Discrete variables consist of countable, specific values and include whole numbers.
- Continuous variables are measurable, can take any value within a range, and include real numbers.
Examples of Random Variables
- 'A' represents the sum of numbers when a pair of dice is tossed.
- 'B' represents the distance leaped (in meters) by a long-jumper.
- 'W' represents the length of time (in minutes) a scheduled airplane flight is delayed.
- 'X' represents the number of correct answers on a 10-item True-False test.
- A and X are classified as discrete random variables.
- B and W are classified as continuous random variables.
Probability Distribution Function
- A probability distribution demonstrates the relative likelihood of each outcome in an experiment.
- Consider a football team playing three consecutive games, where 'W' is a win and 'L' is a loss.
- The sample space is the set of all possible outcomes.
- The sample space is {WWW, WWL, WLW, LWW, WLL, LWL, LLW, LLL}.
Sample Point Probabilities
- WWW (3 wins)
- WWL, WLW, LWW (2 wins)
- WLL, LWL, LLW (1 win)
- LLL (0 wins)
Probability Mass Function
- A probability mass function (PMF) assigns a probability to each sample point.
- PMFs can be expressed in tabular, graphical, or formula form.
- The probability of each value of the discrete random variable is between 0 and 1, inclusive.
- The sum of all probabilities equals 1.
Example: Dice Game
- A pair of dice thrown, and the sum of the values determines winning.
- A win occurs with a sum of 3 to 9.
Dice Game Sample Space
- The sample space includes all possible sums from 2 to 12 when throwing two dice.
- 2nd Die (Columns): 1, 2, 3, 4, 5, 6
- 1st Die (Rows): 1, 2, 3, 4, 5, 6
- Sum of the values of the 2 die face up: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
- The number of points within the probability mass function is listed from 1 to 6 then down to 1
Probability Calculation
- The probability of getting a sum of 3 to 9 in the dice game is P(3 ≤ Y ≤ 9).
- P(3 ≤ Y ≤ 9) = 2/36 + 3/36 + 4/36 + 5/36 + 6/36 + 5/36 + 4/36 = 29/36.
- The probability of winning the dice game is 29/36, or approximately 80.56%.
Checkpoint 1: Absolute Value of Dice Differences
- Objective: Construct the probability mass function (PMF) of Y and compute related probabilities in an experiment involving rolling a pair of dice.
- Y represents the random variable of the absolute value of the difference of the numbers that come up.
- Find the probability of randomly getting an absolute value that is (a) two, (b) at most three, and (c) between two and five.
- Six possible values of Y are: 0, 1, 2, 3, 4, and 5 – each from 36 sample points.
Expected Value (Mean) of a Discrete Random Variable
- The mean (μ) of a random variable, also known as the expected value (E), represents the anticipated average outcome over many trials.
- For a discrete random variable X, the expected value is calculated as E(X) = μ = Σ [xi * P(xi)], where xi is each value of X.
- To calculate the mean, multiply each value of X by its corresponding probability and add the products.
Variance and Standard Deviation
- Variance measures the spread of different values about the mean.
- Alternative formula: σ² = μ(Χ2) – (μ(Χ))^2
- Standard deviation is the square root of the variance (σ = √σ²).
Example: Reunion Game Fair Price
- A high school reunion committee organizes a game with 150 balls in a box to raise funds.
- The ball values includes ₱500, ₱1000, ₱5000 and ₱0
- 10 balls win ₱500, 5 win ₱1000, 1 wins ₱5000, and 134 win nothing.
Solution
- Define A is the random variable that represents the amount a player can win.
- Then, A can take on the values 500, 1000, 5000, and 0.
- These values of A, represent the random variable multiplied by its relevant propbability with the corresponding result
- E(A) = 0*(67/75) + 500*(1/15) + 1000*(1/30) + 5000*(1/150) = 100
- A fair price to play this game is Php100.
Example 2: Car Insurance
- A car insurance company pays out Php500,000 for a stolen or destroyed car.
- The insurance policy costs Php24,000.
- The company pays out 0.002 percent of the time.
Solution
- Define X as the owner's net gain with possible values
- The payout is 476,000 and the loss is -24,000
- The value of X= 476,000 with 0.002 probability
- The value of X= −24,000 with 0.998 probability (1-0.002)
- Calculate the expect value for the insurance company:
- E(X) = (476,000)(0.002) + (-24,000)(0.998) = −23,000
- The policy favors the company, not the owner.
Example 4: Absolute Difference of Dice
- Consider random variable Y, which is the absolute value of the difference between the numbers when rolling a pair of dice.
- The expected value of Y is approximately 1.94.
- The variance of Y is approximately 2.05.
- Standard deviation of Y = √2.05 ≈ 1.43.
Binomial Distribution
- Describes a distribution with only two possible outcomes.
- p = probability of success
- q = probability of failure
- n = number of trials
- Formula P(x) = C(n, r) *p^x * q^(n-x), where C(n, r) = n! / (r!(n-r)!).
Poisson Distribution
- Models how many times an event is likely to occur over a specified period.
- Lambda is equal to the expected value (EV) of x when that is also equal to its variance.
- e is Euler's number (e = 2.71828...)
- x is the number of occurrences
- x! is the factorial of x
- Formula P(X) = (λ^x * e^-λ) / X!
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.