Podcast
Questions and Answers
What is the particular solution of the equation $u_n = 3u_{n-1} - 2u_{n-2} = 3n$?
What is the particular solution of the equation $u_n = 3u_{n-1} - 2u_{n-2} = 3n$?
b = 2
What is the particular solution for the equation $u_n + 7u_{n-1} + 10u_{n-2} = 5$?
What is the particular solution for the equation $u_n + 7u_{n-1} + 10u_{n-2} = 5$?
a = 18
What are the values of a and b in the particular solution for the equation $u_n - 8u_{n-1} + 7u_{n-2} = 2n - 6$?
What are the values of a and b in the particular solution for the equation $u_n - 8u_{n-1} + 7u_{n-2} = 2n - 6$?
a = -1/6, b = 4/9
What is the value of b in the particular solution for the equation $u_{n+1} - 3u_n + 2u_{n-1} = 6(-1)^n$?
What is the value of b in the particular solution for the equation $u_{n+1} - 3u_n + 2u_{n-1} = 6(-1)^n$?
Signup and view all the answers
What is the particular solution for the equation $u_n + 4u_{n-1} + 4u_{n-2} = 7$?
What is the particular solution for the equation $u_n + 4u_{n-1} + 4u_{n-2} = 7$?
Signup and view all the answers
What is the particular solution for the equation $u_n - 7u_{n-1} + 10u_{n-2} = 6n + 8$?
What is the particular solution for the equation $u_n - 7u_{n-1} + 10u_{n-2} = 6n + 8$?
Signup and view all the answers
What is the complementary solution for the equation $u_n = 3u_{n-1} + 2n$?
What is the complementary solution for the equation $u_n = 3u_{n-1} + 2n$?
Signup and view all the answers
What is the particular solution of the equation $u_n = 2u_{n-1} + 3n$?
What is the particular solution of the equation $u_n = 2u_{n-1} + 3n$?
Signup and view all the answers
What is the value of x in the complementary solution for the equation $u_n = 4u_{n-1} + 4n$?
What is the value of x in the complementary solution for the equation $u_n = 4u_{n-1} + 4n$?
Signup and view all the answers
Write out the first 5 terms of the sequence defined as follows: $u_n = 2u_{n−1} + 5$ where $u_1 = 3$.
Write out the first 5 terms of the sequence defined as follows: $u_n = 2u_{n−1} + 5$ where $u_1 = 3$.
Signup and view all the answers
Find $u_3$ given that $u_{n+2} = 4u_{n+1} + u_n$ where $u_0 = 5$ and $u_1 = 8$.
Find $u_3$ given that $u_{n+2} = 4u_{n+1} + u_n$ where $u_0 = 5$ and $u_1 = 8$.
Signup and view all the answers
Form a difference equation to represent the deer population after each year if the population is estimated to be 1000 and increases by 15% each year.
Form a difference equation to represent the deer population after each year if the population is estimated to be 1000 and increases by 15% each year.
Signup and view all the answers
Form a difference equation for a credit card balance that owes €500 with a 3% monthly interest and a €50 payment each month.
Form a difference equation for a credit card balance that owes €500 with a 3% monthly interest and a €50 payment each month.
Signup and view all the answers
Model the weekly number of infected people caused by a virus that lays dormant for a week and infects an average of 3 people per week.
Model the weekly number of infected people caused by a virus that lays dormant for a week and infects an average of 3 people per week.
Signup and view all the answers
What is the steady state of the fish population modeled by $u_{n+1} = 0.6u_n + 800$ where $u_0 = 300$?
What is the steady state of the fish population modeled by $u_{n+1} = 0.6u_n + 800$ where $u_0 = 300$?
Signup and view all the answers
Write the difference equation for the deer population that increases by 8% naturally but 2000 deer are killed each year.
Write the difference equation for the deer population that increases by 8% naturally but 2000 deer are killed each year.
Signup and view all the answers
Calculate when the deer population will die out based on the difference equation $u_{n+1} = 1.08u_n - 2000$.
Calculate when the deer population will die out based on the difference equation $u_{n+1} = 1.08u_n - 2000$.
Signup and view all the answers
What should be the maximum number of deer hunted per year to not kill the entire population?
What should be the maximum number of deer hunted per year to not kill the entire population?
Signup and view all the answers
Write a difference equation to show the amount of money in the savings account after n months with €2000 initial deposit, 0.2% interest, and €120 deposit each month.
Write a difference equation to show the amount of money in the savings account after n months with €2000 initial deposit, 0.2% interest, and €120 deposit each month.
Signup and view all the answers
How much will be in the account after 3 years based on the difference equation $u_{n+1} = 1.002u_n + 120$?
How much will be in the account after 3 years based on the difference equation $u_{n+1} = 1.002u_n + 120$?
Signup and view all the answers
Write the difference equation for a loan of €2500 with yearly interest rate of 5% and monthly payments of €200.
Write the difference equation for a loan of €2500 with yearly interest rate of 5% and monthly payments of €200.
Signup and view all the answers
Solve the difference equation $u_{n+1} = 5u_n + 4$ where $u_0 = 1$.
Solve the difference equation $u_{n+1} = 5u_n + 4$ where $u_0 = 1$.
Signup and view all the answers
What is the maximum monthly payment needed to eliminate the loan modeled by $u_{n+1} = 1.004u_n - x$ where $u_0 = 2500$?
What is the maximum monthly payment needed to eliminate the loan modeled by $u_{n+1} = 1.004u_n - x$ where $u_0 = 2500$?
Signup and view all the answers
For a mortgage of €230,000 at a monthly interest rate of 0.03%, using a difference equation, find the monthly repayment amount.
For a mortgage of €230,000 at a monthly interest rate of 0.03%, using a difference equation, find the monthly repayment amount.
Signup and view all the answers
Study Notes
Difference Equations - Introduction
- Difference equations are equations that define sequences based on previous terms.
- Recurrence relations are a specific type of difference equation where a term is calculated using preceding terms.
Recurrence Relations
- Example: (u_n = 2u_{n-1} + 5) with (u_1 = 3) defines a sequence where subsequent terms depend on the prior value.
- The order of a difference equation is determined by the range of subscripts involved in the calculation of the new term.
Difference Equations
- Types of equations can be classified as homogeneous (all terms from previous terms) or inhomogeneous (some terms not derived from previous terms).
- Example of a 1st order homogeneous equation: (3u_{n+1} = 4u_n).
- Example of a 2nd order inhomogeneous equation: (2u_{n+2} - 5u_{n+1} = 3u_n + 6).
Forming Difference Equations
- Difference equations can model real-life situations at discrete intervals, e.g., population growth or financial scenarios.
- Example: Deer population increasing by 15% annually can be modeled with (u_n = 1.15 u_{n-1}) with an initial population (P_0 = 1000).
Solving 1st Order Difference Equations
- Process involves transforming the equation to find any term without recursion.
- Common form for a solution: (u_n = xA^n + y).
- Example solution: For (u_n = 3u_{n-1} - 2) with (u_1 = 2), results in a solution of (u_n = (3^n) + 1).
Steady State
- A steady state refers to a situation where the value of a sequence stabilizes as (n) approaches infinity.
- Example: Fish population modeled by (u_{n+1} = 0.6u_n + 800) approaches a steady state of 2000.
Solving Financial Difference Equations
- Financial problems can also be modeled using difference equations, e.g., interest on savings accounts.
- Example: For a savings account with an initial amount €2000 and monthly deposits, the equation is (u_{n+1} = 1.002u_n + 120).
2nd Order Homogeneous Difference Equations
- Steps for solving include forming the characteristic equation, finding roots, and determining the form of the general solution.
- Roots lead to specific equations based on distinct or equal values, influencing the final solution's form.
2nd Order Inhomogeneous Difference Equations
- Solutions consist of a complementary solution and a particular solution.
- Particular solutions are derived based on the nature of (f(n)) in the inhomogeneous equation.
- Example: For (u_n + 6u_{n-1} - 7u_{n-2} = 2n - 6), the form of the particular solution would be (an^2 + bn).
Key Points
- Understanding the differences between homogeneous and inhomogeneous equations is crucial for effective modeling.
- Recognizing roots in characteristic equations helps in determining the overall solution forms.
- Real-life applications such as population dynamics and financial mathematics are successfully modeled with difference equations.### Solving Inhomogeneous Difference Equations
- Particular solutions are inserted into original equations for matching subscripts.
- Coefficients are equated to derive the complete solution.
- The final solution combines complementary and particular components.
Example Question 1
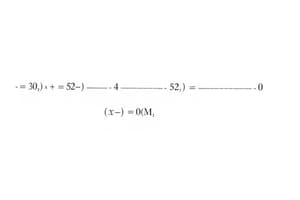
- Equation: (u_{n+1} - 3u_n + 2u_{n-1} = 6(-1)^n)
- Initial conditions: (u_0 = 12), (u_1 = 12)
- Characteristic roots: (x^2 - 3x + 2 = 0) yields roots (x=2) and (x=1).
- Complementary solution form: (x(2)^n + y(1)^n)
- Particular solution hypothesis: (b(-1)^n)
- After coefficient comparison: (b = -1)
- Combined solution: (u_n = -2(2)^n + 15(1)^n - 1(-1)^n)
Example Question 2
- Equation: (u_n + 4u_{n-1} + 4u_{n-2} = 7)
- Initial conditions: (u_0 = 1), (u_1 = 2)
- Characteristic roots derived from (x^2 - 4x + 4 = 0): (x = -2).
- Complementary solution: (x(-2)^n + y(-2)^n)
- Particular solution hypothesis: constant (a).
- Solve (7 = a + 4a + 4a) to get (a = \frac{7}{9}).
- Combined solution: (u_n = x(-2)^n + y(-2)^n + \frac{7}{9}).
Example Question 3
- Equation: (u_n - 7u_{n-1} + 10u_{n-2} = 6n + 8)
- Initial conditions: (u_0 = 1), (u_1 = 2).
- Characteristic roots from (x^2 - 7x + 10 = 0): (x=5) and (x=2).
- Complementary solution: (x(5)^n + y(2)^n)
- Particular form: linear (an + b).
- Solve to find (a = 2) and (b = 8).
- Final solution: (u_n = 2(5)^n - 9(2)^n + 2n + 8).
1st Order Inhomogeneous Difference Equations
- General form: (u_n = Au_{n-1} + f(n)).
- Solution type: sum of complementary and particular solutions.
- Roots determine the form of the complementary solution.
Characteristic Roots and Particular Solutions
- For non-repeated roots: [a_n, A \neq 1 \Rightarrow a_n]
- For quadratic forms:
- (a n^2 + bn + c \Longrightarrow an^2 + bn + c) if (A \neq 1)
- Increase degree if (A=1).
- Multiply particular solution by (n) if terms overlap with the complementary solution.
Application Examples
- Example equation: (u_n = 3u_{n-1} + 2n)
- Aim: derive constants from particular solution forms to finalize (u_n).
- Systematic approach includes validating the particular solution and combining it with the complementary solution for the full expression.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Related Documents
Description
Explore the fundamentals of difference equations in this comprehensive quiz. Topics include recurrence relations, forming and solving first and second order difference equations, and financial mathematics applications. Test your understanding of these key mathematical concepts.
