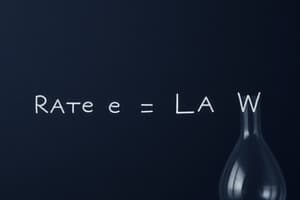Chemical Kinetics: Rate Laws and Reaction Orders

• Chemical kinetics studies reaction rates and factors that influence them.

Reaction Rate

• Defined as the change in reactant or product concentration over time.
• For $aA + bB \rightarrow cC + dD$, Rate $= -\frac{1}{a} \frac{\Delta[A]}{\Delta t} = -\frac{1}{b} \frac{\Delta[B]}{\Delta t} = \frac{1}{c} \frac{\Delta[C]}{\Delta t} = \frac{1}{d} \frac{\Delta[D]}{\Delta t}$

Rate Law

• An equation relating reaction rate to reactant concentrations raised to certain powers.
• General form: Rate $= k[A]^m[B]^n$, $k$ is the rate constant, $m$ and $n$ are reaction orders.
• Overall reaction order is the sum of individual orders ($m + n$).
• Determined experimentally, not from reaction stoichiometry.

Common Rate Laws

• Zero-Order: Rate $= k$; rate is independent of reactant concentration.
• First-Order: Rate $= k[A]$; rate is directly proportional to reactant concentration.
• Second-Order: Rate $= k[A]^2$ or Rate $= k[A][B]$; rate is proportional to the square of one reactant or the product of two.

Temperature Dependence

• Arrhenius Equation: $k = Ae^{-\frac{E_a}{RT}}$; relates rate constant to temperature.
• $A$ is pre-exponential factor, $E_a$ is activation energy, $R$ is gas constant (8.314 J/(mol⋅K)), $T$ is absolute temperature in Kelvin.
• Activation Energy ($E_a$): Minimum energy for a reaction to occur; higher $E_a$ results in slower rate.

Catalysis

• A catalyst speeds up a reaction without being consumed.
• Homogeneous catalysis: Catalyst and reactants are in the same phase.
• Heterogeneous catalysis: Catalyst and reactants are in different phases.

Reaction Mechanisms

• A reaction mechanism is a series of elementary steps from reactants to products.
• An elementary step is a single step where rate law can be derived from stoichiometry.
• The rate-determining step is the slowest step, governing overall reaction rate.

Floyd-Warshall Algorithm

• Used to find the shortest paths between all pairs of vertices in a graph.
• Input is a graph $G = (V, E)$ with edge weights $w: E \rightarrow \mathbb{R}$ and adjacency matrix $D$. $D$ is initialized such that:
  • $d_{ij} = w(i, j)$ if edge $(i, j) \in E$
  • $d_{ij} = \infty$ if edge $(i, j) \notin E$
  • $d_{ij} = 0$ if $i = j$
• Output is a distance matrix $D^* = (d_{ij}^)$, where $d_{ij}^$ is the length of the shortest path from $i$ to $j$.
• Algorithm:
  • for $k$ from 1 to $|V|$:
  • for $i$ from 1 to $|V|$:

  • for $j$ from 1 to $|V|$:
    

  •   $D[i][j] := \min(D[i][j], D[i][k] + D[k][j])$
    

• The algorithm guarantees shortest paths when there are no negative cycles.
• Time Complexity: $\Theta(|V|^3)$
• Space Complexity: $\Theta(|V|^2)$
• The algorithm works with negative edge weights, but not negative cycles.
• The presence of negative cycles are indicated with negative values on the diagonal ($D[i][i] < 0$).

Lecture 24: Photodiodes

• Photodiodes convert light into electrical current.
• Light can be a source of energy.
  • Photovoltaic effect: Light shines on a semiconductor, generating electron-hole pairs.
• Electron-hole pairs will recombine without a potential field.
• Separation of electron-hole pairs by a potential barrier creates a voltage.
  • Photodiodes efficiently collect light-generated carriers.
  • Light-generated carriers are collected to produce current under reverse bias.
  • Current increases linearly with light intensity.
  • Photodiodes typically operate in reverse bias.
• Structure
  • Basic structure: P-N junction.
  • Light shone on the intrinsic region to create electron-hole pairs.
  • Improved structure: p-i-n photodiode
    • Intrinsic (i) region between p and n regions to increase absorption volume.
• Responsivity ($\Re$): Ratio of photocurrent ($I_{ph}$) to incident optical power ($P_{opt}$).
  • Represents effectiveness: $\qquad \Re = \frac{I_{ph}}{P_{opt}}$
• Quantum efficiency ($\eta$): Number of electron-hole pairs generated per incident photon $\qquad \eta = \frac{I_{ph}/q}{P_{opt}/hv} = \frac{\text{Number of electron-hole pairs}}{\text{Number of incident photons}}$
• Avalanche Gain (M): $\qquad M = \frac{I_M}{I_{ph}}$
• Key performance parameters:
  • Responsivity: Sensitivity measure.
  • Speed: Limited by transit time.
  • Dark Current: Current when there is no light.
  • Noise: Random current fluctuations.
  • Capacitance: Can limit speed.
• Advantages
  • High sensitivity, fast response, low noise, small size, low cost
• Disadvantages
  • Temperature dependence, dark current, capacitance, fragility
• Photodiodes can be used;
  • Detect presence/absence of light.
  • Light measurement.
  • Medical imaging, etc.

Markdown Quickstart

• Markdown simplifies text formatting for the web.

Markdown Syntax

Headers

## Heading Level 1
## Heading Level 2
### Heading Level 3

Emphasis

- Italic text*
- *Bold text**
- **Bold italic text***

Lists

• Ordered lists use numbers:

1. First item
2. Second item

• Unordered lists use asterisks or hyphens:

- First item
- Second item

Links

[Link text](URL)

Images

![Alt text](image URL)

Code

• Inline code is enclosed in backticks: printf()
• Code blocks are enclosed in triple backticks:

\`\`\`python
print("Hello, world!")
\`\`\`

Block Quotes

> This is a block quote.

Horizontal Rule

- --

Tables

• Tables require defined headers and separator lines:

| Header 1 | Header 2 |
| -------- | -------- |
| Cell 1   | Cell 2   |

Mathematical Formulas

• Mathematical formulas use LaTeX.

Inline: \(x = y + 2\)
Block: \[ f(x) = \int_{-\infty}^{\infty} \hat{f}(\xi) e^{2 \pi i \xi x} \, d\xi \]

Chemical Kinetics: Rate Details

Rate $= -\frac{1}{a} \frac{d[A]}{dt} = -\frac{1}{b} \frac{d[B]}{dt} = \frac{1}{c} \frac{d[C]}{dt} = \frac{1}{d} \frac{d[D]}{dt}$ where:

• $a, b, c, d$ are stoichiometric coefficients. Reaction Rate Law:
• Rate $= k[A]^x [B]^y$
• Where $k =$ rate constant
• $x =$ reaction order w.r.t $A$
• $y =$ reaction order w.r.t $B$
• $x + y =$ overall reaction order Zero Order Reaction:
• Rate $= k[A]^0 = k$
• $A \rightarrow Products$
• $-\frac{d[A]}{dt} = k$
• $[A] = [A]_0 - kt$
• $t_{1/2} = \frac{[A]_0}{2k}$ First Order Reaction:
• Rate $= k[A]^1 = k[A]$
• $A \rightarrow Products$
• $-\frac{d[A]}{dt} = k[A]$
• $\ln[A] = \ln[A]_0 - kt$
• $t_{1/2} = \frac{0.693}{k}$ Second Order Reaction:
• Rate $= k[A]^2$
• $A \rightarrow Products$
• $-\frac{d[A]}{dt} = k[A]^2$
• $\frac{1}{[A]} = \frac{1}{[A]_0} + kt$
• $t_{1/2} = \frac{1}{k[A]_0}$

Arrhenius Equation

• $k = A e^{-E_a/RT}$
• $E_a$ = activation energy.
• $R$ = gas constant (8.314 J/mol·K)
• $A$ = frequency factor.
• $\ln(\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2})$

### Notable Products

• Binomial Square:

  • $(a + b)^2 = a^2 + 2ab + b^2$
  • $(a - b)^2 = a^2 - 2ab + b^2$

• Conjugate Binomials:

• $(a + b)(a - b) = a^2 - b^2$

• Binomial with Common Term:

• $(x + a)(x + b) = x^2 + (a + b)x + ab$

• Binomial Cube:

• $(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$

• $(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$

{## Factorization

• Common Factor:
• $ab + ac = a(b + c)$
• Difference of Squares:
• $a^2 - b^2 = (a + b)(a - b)$
• Perfect Square Trinomial:
• $a^2 + 2ab + b^2 = (a + b)^2$
• $a^2 - 2ab + b^2 = (a - b)^2$
• Trinomial of the form $x^2 + bx + c$:
• $x^2 + bx + c = (x + p)(x + q)$, where $p + q = b$ and $pq = c$
• Sum or Difference of Cubes:
• $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
• $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$ Basic Markdown Syntax: Markdown is a straightforward way to format text on the web. Headers:
• # Heading 1, ## Heading 2, etc., create headers of different sizes. Emphasis:
• *italic* or _italic_ for italic text. **bold** or __bold__ for bold text. Lists:
• Ordered: 1. First item, 2. Second item
• Unordered: - Item, * Item Links:
• Link text creates a hyperlink. Images:
• ![Alt text](Image URL) embeds an image. Code:
• Inline code: printf() is an example. Block code are enclosed in triple backticks. Blockquotes:
• Use > to create blockquotes. Horizontal Rules:
• --- creates a horizontal line. Tables: | Header 1 | Header 2 | | -------- | -------- | | Cell 1 | Cell 2 |

Static Equilibrium

Static equilibrium means an object is at rest and remains at rest.

• The object has zero translational and rotational acceleration. For translational equilibrium: $\sum \overrightarrow{F} = 0$
• In component form: $\sum F_x = 0$ and $\sum F_y = 0$ For rotational equilibrium: $\sum \tau = 0$ (sum of the torques acting on the body must be equal to zero) Torque Formula: $\tau = rF\sin\theta$ where:
• $r$ is the distance from the axis of rotation to the point where the force is applied.
• $F$ is the magnitude of the force.
• $\theta$ is the angle between the force vector and the vector