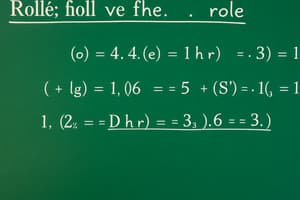Calculus Review Exercises: Analysis

Exercices de révision (II) - Analyse

Exercice 1

• Given a twice-differentiable function $f: \mathbb{R} \rightarrow \mathbb{R}$ and three real numbers $a < b < c$ such that $f(a) = f(b) = f(c)$.
• There exists $\alpha \in ]a, c[$ such that $f'(\alpha) = 0$ and $\beta \in ]a, c[$ such that $f''(\beta) = 0$.
• By Rolle's theorem, since $f(a) = f(b)$, there exists $\alpha_{1} \in ]a, b[$ such that $f'(\alpha_{1}) = 0$.
• By Rolle's theorem, since $f(b) = f(c)$, there exists $\alpha_{2} \in ]b, c[$ such that $f'(\alpha_{2}) = 0$.
• Since $f'(\alpha_{1}) = f'(\alpha_{2}) = 0$, there exists $\beta \in ]\alpha_{1}, \alpha_{2}[$ such that $f''(\beta) = 0$.

Exercice 2

• Finding the following limits

• $\lim_{x \rightarrow 0} \frac{\sin(x) - x}{x^3} = -\frac{1}{6}$

  • Using L'Hôpital's rule twice:
    • First application: $\lim_{x \rightarrow 0} \frac{\sin(x) - x}{x^3} = \lim_{x \rightarrow 0} \frac{\cos(x) - 1}{3x^2}$
    • Second application: $\lim_{x \rightarrow 0} \frac{\cos(x) - 1}{3x^2} = \lim_{x \rightarrow 0} \frac{-\sin(x)}{6x} = -\frac{1}{6}$

• $\lim_{x \rightarrow +\infty} \frac{x^2}{e^x} = 0$

  • Using L'Hôpital's rule twice:
    • First application: $\lim_{x \rightarrow +\infty} \frac{x^2}{e^x} = \lim_{x \rightarrow +\infty} \frac{2x}{e^x}$
    • Second application: $\lim_{x \rightarrow +\infty} \frac{2x}{e^x} = \lim_{x \rightarrow +\infty} \frac{2}{e^x} = 0$

Exercice 3

• Study the nature of the following integrals

• $\int_{0}^{1} \frac{1}{\sqrt{x}} dx$ converges to 2.

  • The function $f(x) = \frac{1}{\sqrt{x}}$ is continuous on $]0, 1]$.
  • Evaluation shows: $\lim_{a \rightarrow 0^{+}} \int_{a}^{1} \frac{1}{\sqrt{x}} dx = \lim_{a \rightarrow 0^{+}} [2\sqrt{x}]_{a}^{1} = 2$

• $\int_{1}^{+\infty} \frac{1}{x^2} dx$ converges to 1.

  • The function $f(x) = \frac{1}{x^2}$ is continuous on $[1, +\infty[$.
  • Evaluation shows: $\lim_{b \rightarrow +\infty} \int_{1}^{b} \frac{1}{x^2} dx = \lim_{b \rightarrow +\infty} [-\frac{1}{x}]_{1}^{b} = 1$

Exercices de révision (II) - Algèbre linéaire

Exercice 4

• $A=\left(\begin{array}{ccc}1 & 2 & 3 \ 2 & 1 & 0 \ -1 & 0 & 2\end{array}\right)$.

• Calculating the determinant of matrix A

  • $\operatorname{det}(A)=1 \cdot(1 \cdot 2-0 \cdot 0)-2 \cdot(2 \cdot 2-0 \cdot(-1))+3 \cdot(2 \cdot 0-1 \cdot(-1))=2-8+3=-3$

• Matrix A is invertible since $\operatorname{det}(A) \neq 0$.

  • $A^{-1}=\frac{1}{\operatorname{det}(A)} \cdot \operatorname{adj}(A)=\frac{1}{-3} \cdot\left(\begin{array}{ccc}2 & -4 & 3 \ -4 & 5 & 6 \ 1 & -2 & -3\end{array}\right)=\left(\begin{array}{ccc}-\frac{2}{3} & \frac{4}{3} & -1 \ \frac{4}{3} & -\frac{5}{3} & -2 \ -\frac{1}{3} & \frac{2}{3} & 1\end{array}\right)$

Exercice 5

• $A=\left(\begin{array}{ll}1 & 2 \ 2 & 1\end{array}\right)$.

• Calculate the eigenvalues of $A$.

  • $\operatorname{det}(A-\lambda I)=\left|\begin{array}{cc}1-\lambda & 2 \ 2 & 1-\lambda\end{array}\right|=(1-\lambda)^{2}-4=\lambda^{2}-2 \lambda-3=(\lambda-3)(\lambda+1)$
  • The eigenvalues of $A$ are $\lambda_{1}=3$ and $\lambda_{2}=-1$.

• Determine the eigenvectors associated with each eigenvalue.

  • For $\lambda_{1}=3$, we seek vectors $v=\left(\begin{array}{l}x \ y\end{array}\right)$ such that $(A-3 I) v=0$, i.e., $\left(\begin{array}{cc}-2 & 2 \ 2 & -2\end{array}\right)\left(\begin{array}{l}x \ y\end{array}\right)=\left(\begin{array}{l}0 \ 0\end{array}\right)$. Thus, $-2 x+2 y=0$, i.e., $x=y$.
  • The eigenvectors associated with $\lambda_{1}=3$ are thus of the form $v=\left(\begin{array}{l}x \ x\end{array}\right)$, with $x \neq 0$.
  • For $\lambda_{2}=-1$, we seek vectors $v=\left(\begin{array}{l}x \ y\end{array}\right)$ such that $(A+I) v=0$, i.e., $\left(\begin{array}{ll}2 & 2 \ 2 & 2\end{array}\right)\left(\begin{array}{l}x \ y\end{array}\right)=\left(\begin{array}{l}0 \ 0\end{array}\right)$. Thus, $2 x+2 y=0$, i.e., $x=-y$.
  • The eigenvectors associated with $\lambda_{2}=-1$ are thus of the form $v=\left(\begin{array}{c}x \ -x\end{array}\right)$, with $x \neq 0$.

Algorithmic Trading and Order Book Dynamics

Algorithmic Trading

• A subset of electronic trading that uses algorithms to automate trading strategies.
• Electronic trading gained traction in the 1970s as automated order execution became more prevalent.

Categories of Algorithmic Trading

• Execution Algorithms:
  • To minimize transaction costs related to risk
  • Examples include VWAP, TWAP and implementation shortfall
• Market Making Algorithms:
  • To quote strategically to capture spread
  • Examples include inventory management models and queueing models
• Statistical Arbitrage:
  • To exploit temporary statistical mispricings
  • Examples include pairs trading and index arbitrage
• High-Frequency Trading (HFT):
  • A subset of algorithmic trading characterised by ultra-low latency, high message rates and short-term positions

Order Book

• Electronic list of buy and sell orders
• Organized by price level.
• Includes Limit orders:
  • Buy or sell at a specified price or better.
• Market orders:
  • Buy or sell immediately.
• Order Book Events include:
  • Limit order arrival
  • Limit order cancellation
  • Market order arrival and trade execution
  • Hidden orders

Order Book Dynamics

• Order book states change over time due to order submissions, cancellations, and executions.
• Order Book Imbalance:
  • Measure of buying and selling pressure.
• Mid-Price Dynamics:
  • The average of the best bid and offer prices.
• Order Book as a Queue:
  • Can be modeled as a queueing system.
• Order Book and Price Discovery:
  • Defines the equilibrium price of a security.

Further Resources

• Some academic and online resources for further study include:
  • Books like "Algorithmic Trading and DMA" by Barry Johnson, "Quantitative Trading" by Ernest Chan and "Advances in Financial Machine Learning" by Marcos Lopez de Prado
  • APIs like the interactive broker API and the Binance API
  • Languages like Python, R, Java

Chemical Kinetics

Reaction Rate

• Measuring the rate and factors affecting chemical reactions:
  • Reaction rate is the speed at which reactants turn into products, typically measured as the change in concentration per unit time.
  • The rate law expresses the relationships between the reaction rate and the concentrations of reactants.
  • Using the general reaction $aA + bB \rightarrow cC + dD$
  • $rate = k[A]^m[B]^n$, ($k$ is the rate constant, $[A]$ and $[B]$ are reactant concentrations, $m$ and $n$ are reaction orders). Rate order defines the dependency of reaction concentrations.

Factors affecting reaction rate

• Concentration of reactants
• Temperature
• Surface Area
• Catalysts
• Pressure

Rate Constant

• Rate constant (k) relates reaction rate and reactant concentrations, specific to each reaction at a given temperature.
• The Arrhenius equation describes k's temperature dependence:
  • The equation being $k = Ae^{-\frac{E_a}{RT}}$
  • ($A =$ pre-exponential, $E_a$ is the activation energy, $R$ = gas constant, $T$ = temperature).

Reaction Mechanisms

• Details pathway of reaction in elementary steps.
• Rate-determining step:
  • Slowest step
  • Determines overall rate.
• Intermediates form in one step and are consumed in a later step, not included in the balanced equation.

Catalysis

• Homogenous catalysis:
  • Catalysts are in the same phase as reactants.
• Heterogenous catalysis:
  • Catalysts are in a different phase than reactants.
• Enzymes are biological catalysts that increase the rate of biochemical reactions.

Examples

• Reactions of nitrogen-dioxide, hydrogen-peroxide and the Haber-Bosch process are provided

Lecture 24: The Fourier Transform

Motivation

• Fourier transform links both contionous and discrete variables.
• Aperiodic Fourier Transform is related to Fourier Series.
• Numerical methods enable the evaluation of fourier and discrete time fourier transforms.

Definition and Equation

• The transform is defined by the formula:
  • $\hat{f}(\xi) = \int_{-\infty}^{\infty} f(x)e^{-2\pi i x \xi}dx$
  • Where $f(x)$ is a function in real space, $\hat{f}(\xi)$ is a function in Fourier space and $\xi$ is the coordinate in Fourier space.
• There is an inversion formula:
  • $f(x) = \int_{-\infty}^{\infty} \hat{f}(\xi)e^{2\pi i x \xi}d\xi$
• Other conventions
  • $\hat{f}(\xi) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(x)e^{-i x \xi}dx$
  • $f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \hat{f}(\xi)e^{i x \xi}d\xi$

Properties

• Linearity: $\mathcal{F}[af(x) + bg(x)] = a\mathcal{F}[f(x)] + b\mathcal{F}[g(x)]$
• Translation: Transform of a translated function. $\mathcal{F}[f(x - a)] = e^{-2\pi i a \xi}\mathcal{F}[f(x)]$
• Modulation: Frequency shift property.$\mathcal{F}[e^{2\pi i a x}f(x)] = \hat{f}(\xi -a)$
• Scaling: Time-scale modification in frequency domain. $\mathcal{F}[f(ax)] = \frac{1}{|a|}\hat{f}(\frac{\xi}{a})$
• Differentiation: $\mathcal{F}[f'(x)] = 2\pi i\xi\hat{f}(\xi)$
• Parseval's Theorem: $\int_{-\infty}^{\infty} |f(x)|^2 dx = \int_{-\infty}^{\infty} |\hat{f}(\xi)|^2 d\xi$

Examples

• Gaussian function $$ f(x) = e^{-\pi x^2} $$

$$ \hat{f}(\xi) = e^{-\pi \xi^2} $$

• Gaussian functions are their own Fourier transforms
• Box function $$ f(x) = \begin{cases} 1, & |x| \leq \frac{1}{2} \ 0, & |x| > \frac{1}{2} \end{cases} $$

$$ \hat{f}(\xi) = \frac{\sin(\pi \xi)}{\pi \xi} $$

• Transforms into a sinc function.

Funciones vectoriales de una variable real

Introducción

• Es una función que asigna a cada número real un vector.
• Describe curvas en el espacio.

Definición

• $\vec{r}(t) = f(t)\hat{i} + g(t)\hat{j} + h(t)\hat{k}$
• Es una función vectorial.
• $f(t)$, $g(t)$ y $h(t)$ son funciones reales de la variable real $t$.
• $\hat{i}$, $\hat{j}$ y $\hat{k}$ son los vectores unitarios en las direcciones $x$, $y$ y $z$, respectivamente.

Dominio

• Es el conjunto de todos los valores de $t$ para los cuales $f(t)$, $g(t)$ y $h(t)$ están definidas.

Límite

• $\lim_{t \to t_0} \vec{r}(t) = \left( \lim_{t \to t_0} f(t) \right) \hat{i} + \left( \lim_{t \to t_0} g(t) \right) \hat{j} + \left( \lim_{t \to t_0} h(t) \right) \hat{k}$
• El vector de limite cuando los limites de $f(t)$, $g(t)$ y $h(t)$ existen

Continuidad

• Una función vectorial $\vec{r}(t)$ es continua en $t = t_0$ si se cumplen las siguientes condiciones:
  1. $\vec{r}(t_0)$ está definida.
  2. $\lim_{t \to t_0} \vec{r}(t)$ existe.
  3. $\lim_{t \to t_0} \vec{r}(t) = \vec{r}(t_0)$.

Derivada de una función vectorial

• Se define como: $\frac{d\vec{r}}{dt} = \lim_{\Delta t \to 0} \frac{\vec{r}(t + \Delta t) - \vec{r}(t)}{\Delta t}$
  • Si existe un limite
• La derivada $\frac{d\vec{r}}{dt}$ es un vector tangente a la curva descrita por $\vec{r}(t)$ en el punto $\vec{r}(t)$.

Reglas de derivación

• Sean $\vec{r}(t)$ y $\vec{s}(t)$ funciones vectoriales diferenciables, y $c$ una constante escalar. Entonces:
  1. $\frac{d}{dt} [c\vec{r}(t)] = c\frac{d\vec{r}}{dt}$
  2. $\frac{d}{dt} [\vec{r}(t) + \vec{s}(t)] = \frac{d\vec{r}}{dt} + \frac{d\vec{s}}{dt}$
  3. $\frac{d}{dt} [\vec{r}(t) \cdot \vec{s}(t)] = \vec{r}(t) \cdot \frac{d\vec{s}}{dt} + \frac{d\vec{r}}{dt} \cdot \vec{s}(t)$
  4. $\frac{d}{dt} [\vec{r}(t) \times \vec{s}(t)] = \vec{r}(t) \times \frac{d\vec{s}}{dt} + \frac{d\vec{r}}{dt} \times \vec{s}(t)$
  5. $\frac{d}{dt} [\vec{r}(f(t))] = \frac{d\vec{r}}{df} \cdot \frac{df}{dt}$

Integral de una función vectorial

• La integral de una función vectorial $\vec{r}(t) = f(t)\hat{i} + g(t)\hat{j} + h(t)\hat{k}$ se define como:
• $\int \vec{r}(t) dt = \left( \int f(t) dt \right) \hat{i} + \left( \int g(t) dt \right) \hat{j} + \left( \int h(t) dt \right) \hat{k}$

Aplicaciones

• Las funciones vectoriales tienen muchas aplicaciones en física e ingeniería, tales como:
• Descripción del movimiento de partículas en el espacio.
• Cálculo de la velocidad y aceleración de un objeto en movimiento.
• Modelado de curvas y superficies.

Guía de inicio rápido

¿Qué es el ecosistema Ocean?

• Es una serie de herramientas para ayudar a las personas a publicar, descubrir y consumir datos con protección de la privacidad
• Permite a los editores de datos monetizar sus datos mientras mantienen la privacidad.
• Permite a los consumidores de datos acceder a más datos de los que podrían obtener de otro modo.

Componentes clave:

• Ocean Market - Mercado de datos descentralizado para la publicación y el consumo.
• Ocean Protocol - Protocolo de código abierto para el intercambio de datos con preservación de la privacidad.
• OCEAN token - Token de utilidad para gobernar la red Ocean y apostar por los datos.

¿Por qué usarlo?

• Para editores de datos:
• Monetización sin renunciar a la privacidad.
• Llegar a un público más amplio de consumidores de datos.
• Mantener el control sobre los datos.
• Para consumidores de datos:
• Acceder a más datos de los que podría obtener de otro modo.
• Asegurar alta calidad de los datos.
• Contribuir a un ecosistema de datos más privado y seguro.

Empezando:

• Obtener el token OCEAN en intercambios de criptomonedas.
• Configurar una billetera para almacenar los tokens y interactuar con Ocean Market.
• Conectarse a Ocean Market a través del sitio web.
• Publicar o consumir datos en Ocean Market.

Próximos pasos:

• Explorar el sitio web y la documentación de Ocean Protocol.
• Unirse a la comunidad de Ocean Protocol.
• Explrar Ocean Market.

Descargo de responsabilidad

• El ecosistema Ocean se encuentra actualmente en fase beta. Úselo bajo su propia responsabilidad.

Chapter 14: Random Variables

Definitions:

• Random variable:
  • A variable whose value is a numerical outcome of a random phenomenon.
• Probability distribution
  • A description of how probabilities are distributed over the values of the random variable.

Discrete Vs Continous Random Variables:

• Discrete Random Variable:
  • Countable number of values.
  • Distributions are $P_i$ between 0 and 1 for each value, summing to 1.
• Continuous Random Variable
  • A continuous random variable X takes all values in an interval of numbers.
  • Probablity determined by areas under a density curve.

Mean of a Discrete Random Variable

• Multiply each possible value by its probability, then sum the products
• The sum of X * the probability of X
• $\mu_x = x_1p_1 + x_2p_2 +... + x_kp_k = \sum x_ip_i$

Standard Deviaiton of a Discrete Random Variable

• Measure the amounts of deviation a random variable experiences from its mean (expected value).
• $\sigma_x = \sqrt{\sum (x_i - \mu_x)^2p_i}$

Rules for means

• If $X$ is a random variable and $a$ and $b$ are fixed numbers, then $\mu_{a+bX} = a + b\mu_X$

• If $X$ and $Y$ are random variables, then $\mu_{X+Y} = \mu_X + \mu_Y$

Rules for Variances

• If $X$ is a random variable and $a$ and $b$ are fixed numbers, then $\sigma_{a+bX}^2 = b^2\sigma_X^2$
• If $X$ and $Y$ are independent random variables, then $\sigma_{X+Y}^2 = \sigma_X^2 + \sigma_Y^2$ $\sigma_{X-Y}^2 = \sigma_X^2 + \sigma_Y^2$

Important

• The rules above are for independent random variables. You cannot measure combined variance for non-independent random variables.

Binomial and Geometric Random Variables

• The Binomial Setting
  • Fixed Number of observations $n$
  • Observations are independent
  • Each Observation categorized as a success or failure.
  • Probability of success $p$ is constant for observation

Binomial and Geometric Random Variables (Cont)

• The count $X$ of successes in a binomial setting has the binomial distribution with parameters $n$ and $p$.
• Binomial Coefficient ${n \choose k} = \frac{n!}{k!(n-k)!}$
• P(X = k) = {n \choose k}p^k(1-p)^{n-k}$ $\mu_X = np$ $\sigma_X = \sqrt{np(1-p)}$

Geometric Setting

• Each Observation categorized as a success or failure.
• Observations are independent
• Probability of success $p$ is constant for observation
• The variable of interest is the number of trials required to obtain the first success.

Geometric Random Variable

• The number of trials $Y$ that it takes to get a success in a geometric setting has the geometric distribution with parameter $p$, the probability of a success on any one trial.
• Geometric Probability Then, $P(Y = k) = (1-p)^{k-1}p$
• If $Y$ is a geometric random variable with probability of success $p$ on each trial, then the mean, or expected value, of the number of trials required to get the first success is $\mu_Y = \frac{1}{p}$

Review exercises covering analysis, including applications of Rolle's theorem and L'Hôpital's rule. Includes finding limits of functions. These exercises are designed to reinforce core calculus concepts.