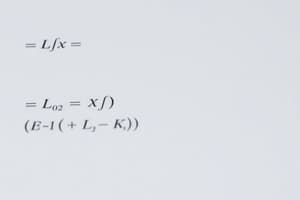Calculus Quiz - Non Calculator and Calculator Sections

Choose a study mode

Play Quiz
Study Flashcards
Spaced Repetition
Chat to Lesson

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the domain of the function f(x) if it is defined as f(x) = undefined?

  • f(x) exists for all real numbers
  • x < -2 or x > 2 (correct)
  • x = -2 or x = 2
  • -2 < x < 2

If g(x) is such that g'(4) = -24, what can you infer about g(4)?

  • g(4) is constant.
  • g(4) is increasing.
  • g(4) is undefined.
  • g(4) is decreasing. (correct)

What value of k will make the function f(x) continuous for all x?

  • There is no real value of k that makes f(x) continuous for all x. (correct)
  • 16
  • 0
  • Any real number

For the function f(x) = 2x² - 7x - 10, what is the absolute maximum value of f(x) on the interval [-1, 3]?

<p>7/4 (A)</p> Signup and view all the answers

What is the acceleration of a particle described by the function s = t³ - 6t² + 9t at time t = 4?

<p>0 (D)</p> Signup and view all the answers

What is the equation of the tangent line to the curve 9x² + 16y² = 52 at the point (2, -1)?

<p>9x - 8y - 26 = 0 (D)</p> Signup and view all the answers

If f(x) = some expression, then f'(x) is most likely related to the:

<p>Original function f(x) (B)</p> Signup and view all the answers

According to the Mean Value Theorem, what is the value c that satisfies the conclusion for f(x) on the interval [2, 5]?

<p>A value not within the interval (C)</p> Signup and view all the answers

What is the correct value of f'(x) if f(x) = 3?

<p>0 (B)</p> Signup and view all the answers

What is the third derivative f'''(x) of the function f(x) = sin(2x)?

<p>-4 sin(2x) (C)</p> Signup and view all the answers

What is the slope of the normal line to y = x + cos(xy) at the point (0, 1)?

<p>-1 (A)</p> Signup and view all the answers

If a 20-foot ladder is sliding down a wall at 5 ft/sec and the top is 10 feet from the floor, how fast is the bottom sliding out?

<p>0.346 (A)</p> Signup and view all the answers

How fast is the distance between Boat A and Boat B increasing after 2.5 hours if Boat A heads North at 12 km/hr and Boat B heads East at 18 km/hr?

<p>31.20 (C)</p> Signup and view all the answers

What is the approximate change in the volume of a sphere when the radius increases from 10 to 10.02 cm?

<p>1256.637 (C)</p> Signup and view all the answers

What is the value of f’(8) if f(x) is defined but not given?

<p>40 (D)</p> Signup and view all the answers

If f(x) is continuous for all real numbers and f(4) = 0, what can be inferred about its continuity at 4?

<p>f(4) is continuous and equals 0 (C)</p> Signup and view all the answers

What is the condition for continuity at the point where f(x) is differentiable if the value of b is what?

<p>0 (C)</p> Signup and view all the answers

What is the local minimum point of the function given in the graph?

<p>(1.66, -0.59) (D)</p> Signup and view all the answers

What can be concluded if f(x) is differentiable everywhere?

<p>f(x) is continuous everywhere (C)</p> Signup and view all the answers

If f(x) = sec x + csc x, what is the correct expression for f’(x)?

<p>sec x tan x - csc x cot x (A)</p> Signup and view all the answers

An equation of the line normal to the graph of y = 3x at the point (2, 4) can be categorized as:

<p>y - 4 = -3(x - 2) (D)</p> Signup and view all the answers

For which value of x does f(x) = x^2 - 4x + 4 have a local minimum?

<p>2 (D)</p> Signup and view all the answers

If f(x) = x^3 - 6x^2 + 9x, which of the following statements is true?

<p>f(x) is continuous everywhere (B)</p> Signup and view all the answers

If f(x) represents a continuous function without breaks, which conclusions are definite?

<p>f(x) is defined everywhere (C)</p> Signup and view all the answers

Flashcards

Derivative of a function

The derivative of a function represents the instantaneous rate of change of the function at a given point.

Domain of a function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. It represents the values that are allowed to be plugged into the function without resulting in undefined results.

Continuity of a function

A function is continuous at a point if the graph of the function can be drawn without lifting the pen. This means that as x approaches a particular value, the function's output approaches a specific value without any gaps or jumps.

Mean Value Theorem

The Mean Value Theorem for Derivatives states that if a function is continuous on a closed interval and differentiable on the open interval, then there exists a point within that interval where the instantaneous rate of change (derivative) equals the average rate of change over the entire interval.

Signup and view all the flashcards

Absolute maximum of a function

The absolute maximum of a function on an interval is the highest value the function attains within that interval.

Signup and view all the flashcards

Implicit differentiation

Implicit differentiation is a technique used to find the derivative of a function that is defined implicitly, meaning the function is not explicitly solved for y in terms of x. It involves taking the derivative of both sides of the equation with respect to x and then solving for dy/dx.

Signup and view all the flashcards

Tangent line to a curve

The equation of a tangent line to a curve at a given point represents a straight line that touches the curve at that point and has the same slope as the curve at that point.

Signup and view all the flashcards

Acceleration of a particle

The acceleration of a particle is the rate of change of its velocity with respect to time. It measures how quickly the velocity of the particle is changing.

Signup and view all the flashcards

Derivative

The derivative of a function f(x) at a point x = a is the slope of the tangent line to the graph of f(x) at that point. It measures the instantaneous rate of change of the function at that point.

Signup and view all the flashcards

Second Derivative

The second derivative of a function f(x), denoted as f''(x), represents the rate of change of the first derivative f'(x). Geometrically, it describes the concavity of the function's graph: positive values indicate upward concavity, negative values indicate downward concavity, and zero values suggest possible inflection points.

Signup and view all the flashcards

Limit

The limit as x approaches a of f(x) exists if and only if both the left-hand limit and the right-hand limit exist and are equal to the same value. This is also known as the two-sided limit.

Signup and view all the flashcards

Discontinuity

A function is considered discontinuous at a point x = a if the limit as x approaches a of the function does not exist, the function is not defined at x = a, or the limit does not equal the value of the function at x = a. This means there's a break, hole, or jump in the graph of the function at that point.

Signup and view all the flashcards

Continuity

A function is considered continuous at a point x = a if the limit as x approaches a of the function exists, the function is defined at x = a, and the limit equals the value of the function at x = a. This means the graph is a smooth curve, without any gaps, jumps or holes.

Signup and view all the flashcards

Local Minimum

A local minimum of a function f(x) occurs at a point x = a if f(a) is less than the function value at all points in a small neighborhood around a. Geometrically, the graph of the function has a dip at x = a.

Signup and view all the flashcards

Local Maximum

A local maximum of a function f(x) occurs at a point x = a if f(a) is greater than the function value at all points in a small neighborhood around a. Geometrically, the graph of the function has a peak at x = a.

Signup and view all the flashcards

Normal Line

A normal line to a curve at a point is a line that is perpendicular to the tangent line at that point. The slope of the normal line is the negative reciprocal of the slope of the tangent line.

Signup and view all the flashcards

Derivative of a Constant

The derivative of a constant is always zero.

Signup and view all the flashcards

Power Rule for Derivatives

The derivative of a power function, f(x) = x^n, is n*x^(n-1).

Signup and view all the flashcards

Derivative of sin(2x)

The derivative of sin(2x) is 2cos(2x).

Signup and view all the flashcards

Slope of Normal Line

The slope of the normal line is the negative reciprocal of the slope of the tangent line.

Signup and view all the flashcards

Finding a Limit

Finding the limit of a function as x approaches a certain value. Here, we simplify the function by factoring and canceling terms.

Signup and view all the flashcards

Finding a Derivative at x=1

Finding the derivative of a function at x=1. Here, we apply the quotient rule and substitute x=1.

Signup and view all the flashcards

Inflection Point

An inflection point is a point on the graph where the concavity changes. To find inflection points, we analyze the second derivative of the function.

Signup and view all the flashcards

Second Derivative at a Value

Finding the second derivative of a function at a specific value. Here, we find the derivative and then take the second derivative, substituting the specified value.

Signup and view all the flashcards

Study Notes

Multiple Choice Questions - Non Calculator Section

  • Question 1: If f(x) = 5x³, then f'(8) = 40
  • Question 2: lim (5x² - 3x + 1) / (4x² + 2x + 5) as x approaches infinity is 5/4
  • Question 3: If f(x) = (3x² + x) / (3x² - x), then f'(x) = (6x² + 1) / (3x² - x)²
  • Question 4: If the function f is continuous for all real numbers and f(x) = (x² - 7x + 12) / (x - 4) when x ≠ 4, then f(4) = 5
  • Question 5: If x² - 2xy + 3y² = 8, then dy/dx = (2x - 2y) / (6y - 2x).
  • Question 6: If f(x) = sec x + csc x, then f'(x) = sec x tan x + csc x cot x
  • Question 7: An equation of the line normal to the graph of y = √(3x² + 2x) at (2, 4) is 4x+7y=36
  • Question 8: If f(x) = cos²x, then f" (π) = -2.
  • Question 9: If f(x) = x² + 1 and g(x) = 3x, then g(f(2)) = 37
  • Question 10: The slope of the line tangent to the graph of 3x² + 5 ln y = 12 at (2, 1) is 12/5

Multiple Choice Questions - Calculator Section

  • Question 11: If f(x) is continuous everywhere for all real numbers x, which of the following must be true?

  • I. f(x) is continuous everywhere

  • II. f(x) is differentiable everywhere

  • III. f(x) has a local minimum at x = 2

  • Answer: I only

  • Question 12: For what value of x does the function f(x) = x³ - 9x² - 120x + 6 have a local minimum?

  • Answer: 10

  • Question 13: lim (sin x cos x - sin x) / x as x approaches 0 is 1

  • Question 14: If f(x) = cos(x + 1), then f' (π) = -3cos²(π +1)sin(n + 1)

  • Question 15: lim (tan(π/6 + h) - tan(π/6)) / h as h approaches 0 is √3

  • Question 16: If g(x) = 3x⁴ - 5x², find g'(4) is -72

  • Question 17: The domain of the function f(x) = √(4 - x²) is -2 ≤ x ≤ 2

  • Question 18: lim (x² - 25) / (x - 5) as x approaches 5 is 10

  • Question 19: Evaluate lim h→0 (5/(5+h)^2 - 5/25) / h is 2

  • Question 20: Find k so that f(x) = (x² - 16) / (x - 4); x ≠ 4, k ; x = 4 is continuous for all x.

  • Answer: k=8

  • Question 21: If f(x) = x² cos 2x, find f '(x).

  • Answer:- 2x cos 2x + 2x²sin 2x

  • Question 22: An equation of the line tangent to y= 4x³ - 7x² at x = 3 is y - 45 = 66(x- 3)

  • Question 23: Find a positive value c for x that satisfies the conclusion of the Mean Value Theorem for Derivatives for f(x) = 3x² − 5x + 1 on the interval [2, 5].

  • Answer: 11/6

  • Question 24: Given f(x) = 2x² - 7x - 10, find the absolute maximum of f(x) on [-1, 3].

  • Answer: -8

  • Question 25: Find dy/dx if x²y + xy² = -10.

  • Answer: (3x²y+y³) / (3x² + 3xy²)

  • Question 26: Find the equation of the tangent line to 9x² + 16y² = 52 through (2, -1).

  • Answer: 9x-8y-26=0

  • Question 27: A particle's position is given by s= t³ - 6t² + 9t. What is its acceleration at time t = 4?

  • Answer: 12

  • Question 28: If f(x) = 3ˣ, then f'(x) = 3ˣ ln 3

  • Question 29: If f(x) = sin²x, find f''(x).

  • Answer: - 4 sin x cos x

  • Question 30: Find the slope of the normal line to y = x + cos xy at (0, 1).

  • Answer: -1

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Quiz Team

Related Documents

Princeton Exam 1-1MPCstsemester[2]dec12-1-4 PDF

More Like This

Use Quizgecko on...
Browser
Open
Browser
Browser