3: Chapter 3: Relationships: Scatterplots and Correlation

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the primary purpose of using scatterplots in biostatistics?

To evaluate relationships between two quantitative variables (correct)

To identify outliers in the dataset

To summarize data with measures of center and spread

To present categorical data visually

What does the correlation coefficient 'r' indicate in a scatterplot analysis?

The direction and strength of the relationship between two variables (correct)

The average value of the two variables involved

The number of data points in the scatterplot

The presence of outliers in the data

In the context of scatterplots, what does adding categorical variables allow analysts to do?

Reduce the complexity of the data being analyzed

Eliminate the need for correlation analysis

Compare groups within the bivariate data (correct)

Focus solely on numerical summaries of data

Which of the following best describes 'bivariate data'?

Data that includes two quantitative variables for each individual Signup and view all the answers

What does the correlation coefficient measure?

The direction and strength of a relationship Signup and view all the answers

In a correlation coefficient of r = -0.75, what does the negative sign indicate?

As one variable increases, the other decreases Signup and view all the answers

Why is the correlation coefficient considered non-resistant to outliers?

It uses means and standard deviations for calculation Signup and view all the answers

What is the range of values for the correlation coefficient?

-1 to 1 Signup and view all the answers

How is the strength of the correlation characterized?

By the absolute value of r Signup and view all the answers

What does the response variable measure in a study?

An outcome of the study. Signup and view all the answers

In the context of scatterplots, what is typically plotted on the x-axis?

The explanatory variable. Signup and view all the answers

Which of the following describes the typical use of a scatterplot?

To illustrate the relationship between bivariate quantitative data. Signup and view all the answers

What should be avoided in the scaling of a scatterplot?

Leaving blank spaces in the plot. Signup and view all the answers

When interpreting scatterplots, which aspect describes how closely the points fit a specific form?

Strength. Signup and view all the answers

What type of relationship is indicated by a scatterplot where points trend upwards from left to right?

Positive correlation. Signup and view all the answers

What does a positive association indicate between two quantitative variables?

High values of one variable are related to high values of the other. Signup and view all the answers

How is an outlier defined in the context of scatterplots?

A data value that has a low probability of occurrence. Signup and view all the answers

What is indicated by a weak or no relationship between two variables?

The values of the two variables do not co-vary consistently. Signup and view all the answers

What best describes the strength of the relationship between two variables?

The amount of variation or scatter around the main pattern. Signup and view all the answers

When adding categorical variables to scatterplots, what effect does it have on understanding relationships?

It helps clarify the relationship by using different symbols for groups. Signup and view all the answers

What can be inferred when a scatterplot shows extreme scatter without a clear pattern?

There might be no meaningful relationship between the variables. Signup and view all the answers

Which scenario best illustrates a negative association between two quantitative variables?

As the unemployment rate rises, consumer spending decreases. Signup and view all the answers

What outcome is typically expected when examining the relationship between incline and energy expended in running speed?

A strong positive association exists for steeper inclines. Signup and view all the answers

Why is it important to identify outliers in a dataset?

Outliers may indicate errors or exceptional cases that affect analyses. Signup and view all the answers

What does positive association typically imply when evaluating two quantitative variables?

An increase in one variable leads to an increase in the other. Signup and view all the answers

Study Notes

Biostatistics & Statistical Analysis - Chapter 3

Chapter 3 focuses on relationships using scatterplots and correlation.
Previous Learning Objectives covered describing distributions using numbers:
- Measures of center (mean and median)
- Measures of spread (quartiles and standard deviation)
- Five-number summary and boxplots
- Interquartile range (IQR) and outliers
- Dealing with outliers
- Choosing among summary statistics
- Organizing statistical problems

Learning Objectives

Demonstrate relationships using scatterplots and correlation
Understand bivariate data
Create scatterplots
Interpret scatterplots
Add categorical variables to scatterplots
Define the correlation coefficient (r)
Understand facts about correlation

Bivariate Data

For each individual, data is recorded on two variables.
Examine relationships between variables.
Changes in one variable often correlate with changes in another.
Example: Number of beers consumed and resulting blood alcohol content (BAC) for 16 students.

Scatterplots

Used to display quantitative bivariate data.
Each variable maps to an axis.
Each individual is represented as a point on the plot.

Explanatory and Response Variables

A response (dependent) variable measures the outcome of a study.
An explanatory (independent) variable influences the response variable
In a scatterplot, explanatory variable is typically plotted on the x-axis.
Example: Number of beers is the explanatory variable (independent variable) and BAC is the response variable (dependent variable)

Scaling a Scatterplot

Data is often displayed similarly across different plots.
Both variables should occupy a similar amount of space.
The plot should be roughly square, points ideally filling the plot space without blank areas.

Interpreting Scatterplots

Describe the overall relationship pattern.
Look for:
- Form (linear, curved, clusters, no pattern)
- Direction (positive, negative, no direction)
- Strength (how closely points fit the form and deviations from it)
- Outliers (points that deviate significantly from the pattern).

Types of Relationships

Linear Relationship: The points show a linear pattern.
No Relationship: The points show little or no connection.
Nonlinear Relationship: A pattern not represented by a straight line.
Positive Association: Higher values of one variable tend to occur with higher values in the other variable.
Negative Association: Higher values of one variable tend to occur with lower values in the other variable.

Outliers in Scatterplots

An outlier is unusual or unexpected data point, with a low probability of occurrence.
Outliers in a scatterplot appear outside the overall pattern of the relationship.

Adding Categorical Variables to Scatterplots

Compare two or more relationships on a single plot by using different symbols for groups of points.
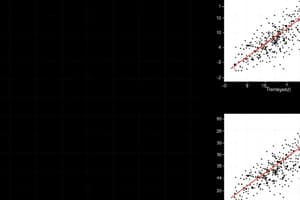
Example: compare thorax length and longevity for male fruit flies that either reproduce or do not reproduce.

The Correlation Coefficient (r)

A measure of the direction and strength of the relationship between two variables.
Calculated using the means and standard deviations of both variables
r = 1 or r =−1 represents a perfect linear relationship
r = 0 represents no linear relationship.

The Roles of the Variables in r

r treats both variables symmetrically (x and y)
One variable can be explanatory for the other, typically put on the x-axis.
The correlation (r) is the same regardless.

r has no units

r isn't influenced by the units of measurement of the variables.
It's a standardized measure.

Correlation and Strength/Direction

Strength is indicated by the absolute value of r.
Direction is indicated by the sign of r (positive or negative).
Range of r: -1 to 1

r is Not Resistant to Outliers

Correlations are based on means & standard deviations, making them sensitive to outliers.
Outliers can influence the correlation value.
In this case, moving a point can reduce the correlation strength.

Software: SPSS

Software for statistical analysis
- Student discount and regular pricing information available online for the appropriate software.

Variance

Another measure of data spread.
Mean sum of squares.
Population vs sample variance formulas.
Standard deviation is the positive square root of variance.

Application of SPSS

A variety of tools, analyses and reporting options.
Data entry, manipulation, and descriptive analyses.

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Description

Test your knowledge on scatterplots in biostatistics with this quiz. Explore concepts such as correlation coefficients, bivariate data, and the interpretation of scatterplots. Assess your understanding of how these graphical tools support statistical analysis.