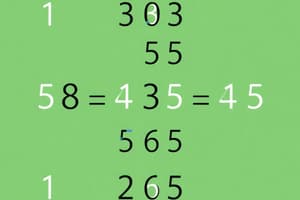Algorithme d'Euclide et PGCD

• L'algorithme d'Euclide est une méthode ancienne et efficace pour calculer le plus grand commun diviseur (PGCD) de deux entiers.
• Le PGCD de deux nombres est le plus grand entier qui se divise sans reste.
• L'algorithme repose sur le principe que le PGCD de deux nombres ne change pas si le plus petit est soustrait du plus grand.

Étapes de l'algorithme d'Euclide :

• Entrée : Deux entiers non négatifs, a et b, où a ≥ b.
• Si b = 0, alors le PGCD est a et l’algorithme se termine.
• Si b ≠ 0, divise a par b et obtiens le reste r.
• Remplace a par b et b par r.
• Retourne à l’étape 2.
• Ce processus se répète jusqu’à ce que le reste soit 0.
• Le dernier reste non nul est le PGCD des deux nombres originaux.
• Exemple : Trouve le PGCD de 270 et 192.
• 270 = 192 * 1 + 78
• 192 = 78 * 2 + 36
• 78 = 36 * 2 + 6
• 36 = 6 * 6 + 0
• Par conséquent, le PGCD (270, 192) = 6.

Implémentation en Python :

• Une fonction gcd(a, b) prend deux entiers comme entrée et retourne leur PGCD.
• La boucle while continue jusqu’à ce que b devienne 0.
• À chaque itération, a est mis à jour avec la valeur de b, et b est mis à jour avec le reste de la division de a par b.
• Lorsque b est 0, la fonction retourne la valeur de a, qui est le PGCD des deux nombres originaux.
• Complexité temporelle : la complexité temporelle est O (log min (a, b)).

Modules pédagogiques de mathématiques

• Une introduction au calcul différentiel.

Faculté des sciences exactes et naturelles et d’arpentage

• Université nationale du Nord-Est.
• Auteurs: Mgter. Stella Maris Ordinas, Dra. Graciela Mabel Salto, Lic. Ana María Cardozo.
• Collaborateurs : Lic. María Mercedes Medina, Lic. José Luis Miño.
• Étudiants en licence de mathématiques : Carlos Daniel Escobar, Mónica Analía Silva.
• Résistance, 2018.
• Ce module vise à faciliter l’apprentissage des concepts de base du calcul différentiel.
• Le calcul différentiel est une branche du calcul qui étudie la façon dont les fonctions changent lorsque leurs variables changent.
• Ce matériel est conçu pour répondre aux besoins des étudiants de la Faculté des sciences exactes et naturelles et d’arpentage de l’Université nationale du Nord-Est.

Table des matières

• Ensembles numériques.
  • Nombres naturels.
  • Nombres entiers.
  • Nombres rationnels.
  • Nombres irrationnels.
  • Nombres réels.
  • Intervalles.
  • Valeur absolue.
• Fonctions réelles.
  • Définition de la fonction.
  • Domaine et image.
  • Graphique d’une fonction.
  • Fonctions linéaires.
  • Fonctions quadratiques.
  • Fonctions polynomiales.
  • Fonctions rationnelles.
  • Fonctions trigonométriques.
  • Fonctions exponentielles et logarithmiques.
  • Opérations avec des fonctions.
  • Composition des fonctions.
• Limite d’une fonction.
  • Idée intuitive de limite.
  • Définition formelle de la limite.
  • Limites latérales.
  • Propriétés des limites.
  • Limites indéterminées.
  • Limites infinies.
  • Asymptotes.
• Continuité d’une fonction.
  • Définition de la continuité.
  • Types de discontinuité.
  • Propriétés des fonctions continues.
• Dérivée d’une fonction.
  • Idée intuitive de la dérivée.
  • Définition de la dérivée.
  • Règles de dérivation.
  • Dérivée des fonctions composées (règle de la chaîne).
  • Dérivation implicite.
  • Dérivées d’ordre supérieur.
• Applications de la dérivée.
  • Ligne tangente et normale.
  • Valeurs maximales et minimales.
  • Croissance et décroissance.
  • Concavité et points d’inflexion.
  • Traçage des courbes.
  • Optimisation.
• Bibliographie.

Ensembles numériques

• Un aperçu des ensembles numériques de base est donné.

Nombres naturels (ℕ)

• Les nombres naturels sont ceux que nous utilisons pour compter : ℕ = {1, 2, 3, 4, 5,...}.

Nombres entiers (ℤ)

• Les nombres entiers incluent les nombres naturels, zéro et les négatifs des nombres naturels : ℤ = {..., -3, -2, -1, 0, 1, 2, 3,...}.

Nombres rationnels (ℚ)

• Les nombres rationnels peuvent être exprimés comme une fraction de deux entiers : ℚ = {a/b | a, b ∈ ℤ, b ≠ 0}.

Nombres irrationnels (𝕀)

• Les nombres irrationnels ne peuvent pas être exprimés comme une fraction de deux entiers (par exemple, √2, π, e).

Nombres réels (ℝ)

• Les nombres réels comprennent à la fois les nombres rationnels et irrationnels et peuvent être représentés sur une ligne de nombres.

Intervalles

• Un intervalle est un ensemble de nombres réels entre deux valeurs données.
  • Intervalle ouvert : (a, b) = {x ∈ ℝ | a < x < b}
  • Intervalle fermé : [a, b] = {x ∈ ℝ | a ≤ x ≤ b}
  • Intervalle semi-ouvert : [a, b) = {x ∈ ℝ | a ≤ x < b}, (a, b] = {x ∈ ℝ | a < x ≤ b}

Valeur absolue

• La valeur absolue d’un nombre réel x, notée |x|, est définie comme : |x| = x si x ≥ 0, |x| = -x si x < 0

Fonctions réelles

Définition de la fonction

• Une fonction f est une règle qui assigne à chaque élément x d’un ensemble A (domaine) un élément unique f(x) d’un ensemble B (codomaine).
• f: A → B

Domaine et image

• Domaine : L’ensemble de toutes les valeurs d’entrée x pour lesquelles la fonction est définie.
• Image : L’ensemble de toutes les valeurs de sortie f(x) qui sont obtenues en appliquant la fonction aux valeurs du domaine.

Diagramme d’une fonction

• Le diagramme d’une fonction f est l’ensemble des paires ordonnées (x, f(x)) dans le plan cartésien.

Fonctions linéaires

• Une fonction linéaire a la forme : f(x) = mx + b où m est la pente et b est l’ordonnée à l’origine.

Fonctions quadratiques

• Une fonction quadratique a la forme : f(x) = ax² + bx + c où a, b et c sont des constantes et a ≠ 0.

Fonctions polynomiales

• Une fonction polynomiale a la forme : f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀ où les aᵢ sont des constantes et n est un entier non négatif.

Fonctions rationnelles

• Une fonction rationnelle est le quotient de deux polynômes : f(x) = P(x) / Q(x) où P(x) et Q(x) sont des polynômes et Q(x) ≠ 0.

Fonctions trigonométriques

• Des exemples de fonctions trigonométriques comprennent : sinus (sin x), cosinus (cos x), tangente (tan x), etc.

Fonctions exponentielles et logarithmiques

• Fonction exponentielle : f(x) = aˣ, où a > 0 et a ≠ 1.
• Fonction logarithmique : f(x) = logₐ(x), où a > 0, a ≠ 1 et x > 0.

Opérations avec des fonctions

• Les fonctions peuvent être additionnées, soustraites, multipliées et divisées :
• (f + g)(x) = f(x) + g(x)
• (f - g)(x) = f(x) - g(x)
• (f · g)(x) = f(x) · g(x)
• (f/g)(x) = f(x) / g(x), à condition que g(x) ≠ 0

Composition des fonctions

• La composition de deux fonctions f et g est définie comme : (f ∘ g)(x) = f(g(x)).

Limite d’une fonction

Idée intuitive de la limite

• La limite d’une fonction f(x) lorsque x s’approche d’une valeur c est la valeur dont f(x) s’approche lorsque x s’approche de c.

Définition formelle de la limite

• La limite de f(x) lorsque x s’approche de c est L si pour tout ϵ > 0, il existe un δ > 0 tel que si 0 < |x - c| < δ, alors |f(x) - L| < ϵ.
• lim (x→c) f(x) = L

Limites latérales

• Limite latérale du côté droit : lim (x→c⁺) f(x)
• Limite latérale du côté gauche : lim (x→c⁻) f(x)

Propriétés des limites

• lim (x→c) [f(x) + g(x)] = lim (x→c) f(x) + lim (x→c) g(x)
• lim (x→c) [f(x) - g(x)] = lim (x→c) f(x) - lim (x→c) g(x)
• lim (x→c) [k · f(x)] = k · lim (x→c) f(x)
• lim (x→c) [f(x) · g(x)] = lim (x→c) f(x) · lim (x→c) g(x)
• lim (x→c) f(x) / g(x) = lim (x→c) f(x) / lim (x→c) g(x), si lim (x→c) g(x) ≠ 0

Limites indéterminées

• Des exemples de formes indéterminées comprennent : 0/0, ∞/∞, 0 · ∞, ∞ - ∞, 1^∞, 0⁰, ∞⁰.

Limites infinies

• lim (x→c) f(x) = ∞
• lim (x→c) f(x) = -∞

Asymptotes

• Asymptote verticale : Si lim (x→c) f(x) = ±∞, alors x = c est une asymptote verticale.
• Asymptote horizontale : Si lim (x→∞) f(x) = L ou lim (x→-∞) f(x) = L, alors y = L est une asymptote horizontale.
• Asymptote oblique : Si lim (x→∞) [f(x) - (mx + b)] = 0 ou lim (x→-∞) [f(x) - (mx + b)] = 0, alors y = mx + b est une asymptote oblique.

Continuité d’une fonction

Définition de la continuité

• Une fonction f est continue en c si :
  • f(c) est défini.
  • lim (x→c) f(x) existe.
  • lim (x→c) f(x) = f(c)

Types de discontinuité

• Discontinuité éliminable : lim (x→c) f(x) existe, mais lim (x→c) f(x) ≠ f(c) ou f(c) n’est pas défini.
• Discontinuité de saut : lim (x→c⁺) f(x) ≠ lim (x→c⁻) f(x)
• Discontinuité infinie : lim (x→c) f(x) = ±∞

Propriétés des fonctions continues

• La somme, la soustraction, le produit et le quotient (si le dénominateur n’est pas zéro) des fonctions continues sont continues.
• La composition des fonctions continues est continue.

Dérivée d’une fonction

Idée intuitive de la dérivée

• La dérivée d’une fonction f(x) à un point x = a représente la pente de la droite tangente au diagramme de f(x) à ce point.

Définition de la dérivée

• La dérivée de f(x) en x est définie comme : f’(x) = lim (h→0) [f(x + h) - f(x)] / h

Règles de dérivation

• Dérivée d’une constante : d/dx (c) = 0
• Dérivée d’une puissance : d/dx (xⁿ) = nxⁿ⁻¹
• Dérivée d’une somme/soustraction : d/dx [f(x) ± g(x)] = f’(x) ± g’(x)
• Dérivée d’un produit : d/dx [f(x) · g(x)] = f’(x)g(x) + f(x)g’(x)
• Dérivée d’un quotient : d/dx [f(x) / g(x)] = [f’(x)g(x) - f(x)g’(x)] / [g(x)]²

Dérivée des fonctions composées (règle de la chaîne)

• Si y = f(u) et u = g(x), alors : dy/dx = dy/du · du/dx

Dérivation implicite

• Utilisée pour dériver des fonctions définies implicitement.

Dérivées d’ordre supérieur

• Les dérivées successives d’une fonction sont : f’’(x), f’’’(x), etc.

Application de la dérivée

Droite tangente et normale

• Droite tangente : y - f(a) = f’(a)(x - a)
• Droite normale : y - f(a) = -1/f’(a) (x - a)

Valeurs maximales et minimales

• Les valeurs maximales et minimales locales se trouvent aux points critiques, où f’(x) = 0 ou f’(x) n’existe pas.

Croissance et décroissance

• Si f’(x) > 0, f(x) croît.
• Si f’(x) < 0, f(x) décroît.

Concavité et points d’inflexion

• Si f’’(x) > 0, f(x) est concave vers le haut.
• Si f’’(x) < 0, f(x) est concave vers le bas.
• Les points d’inflexion se produisent là où la concavité change.

Traçage des droites

• Analyse de : domaine, image, intersections avec les axes, asymptotes, croissance, décroissance, maximales, minimales, concavité et points d’inflexion.

Optimisation

• Problèmes d’optimisation : trouver les valeurs maximales ou minimales d’une fonction sujettes à certaines contraintes.

Bibliographie

• Stewart, James. Cálculo: Trascendentes Tempranas. 7ma Edición. Cengage Learning, 2012.
• Thomas, George B. Cálculo: Varias Variables. 12va Edición. Pearson Educación, 2010.
• Purcell, Edwin J., Varberg, Dale y Rigdon, Steven E. Cálculo. 9na Edición. Pearson Educación, 2007.