z(9+x) - (1-x)6
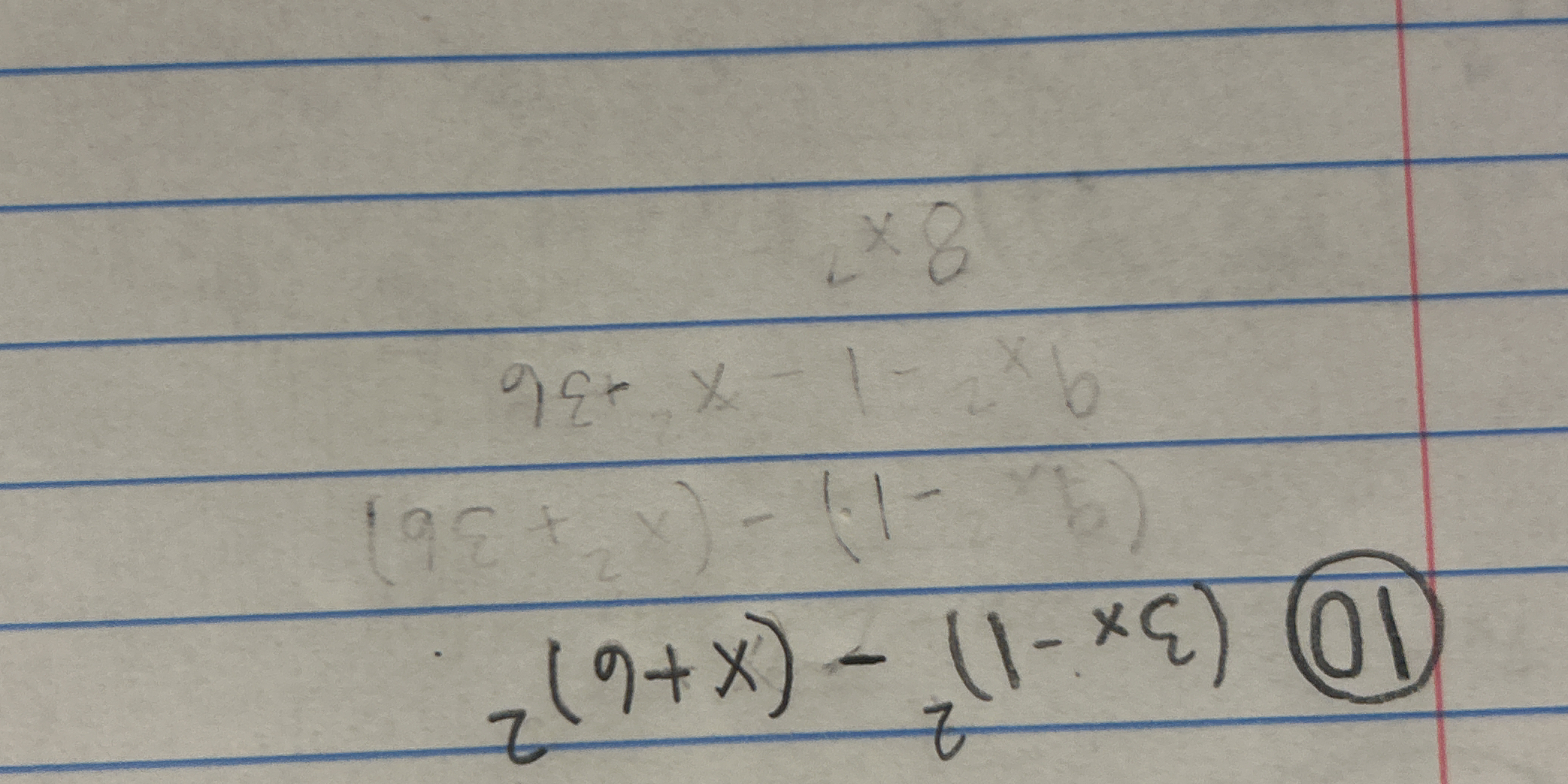
Understand the Problem
The question involves simplifying or solving expressions that include variables and possibly finding a solution or evaluating the expression. It appears to involve algebraic manipulation.
Answer
$$ z(9 + x) + 6x - 6 $$
Answer for screen readers
The simplified expression is: $$ z(9 + x) + 6x - 6 $$
Steps to Solve
-
Expand the expression First, expand the expression $z(9+x)$ and $(1-x)6$ separately.
-
For $z(9+x)$: $$ z(9+x) = 9z + zx $$
-
For $(1-x)6$: $$ (1-x)6 = 6 - 6x $$
-
-
Combine the expanded expressions Now substitute the expanded forms back into the original expression: $$ 9z + zx - (6 - 6x) $$
-
Simplify the expression Distribute the negative sign: $$ 9z + zx - 6 + 6x $$
-
Rearrange the terms Rearrange the terms to group like terms: $$ 9z + zx + 6x - 6 $$
-
Final Expression The final simplified expression is: $$ z(9 + x) + 6x - 6 $$
The simplified expression is: $$ z(9 + x) + 6x - 6 $$
More Information
This expression represents a linear combination of the variables $z$ and $x$, and shows how they relate to each other based on the operations performed. Simplifying expressions is a fundamental skill in algebra that helps in solving equations and working with functions.
Tips
- Not distributing the negative sign correctly while simplifying, which can lead to incorrect terms.
- Forgetting to combine like terms properly, causing an oversight in the final expression.
AI-generated content may contain errors. Please verify critical information