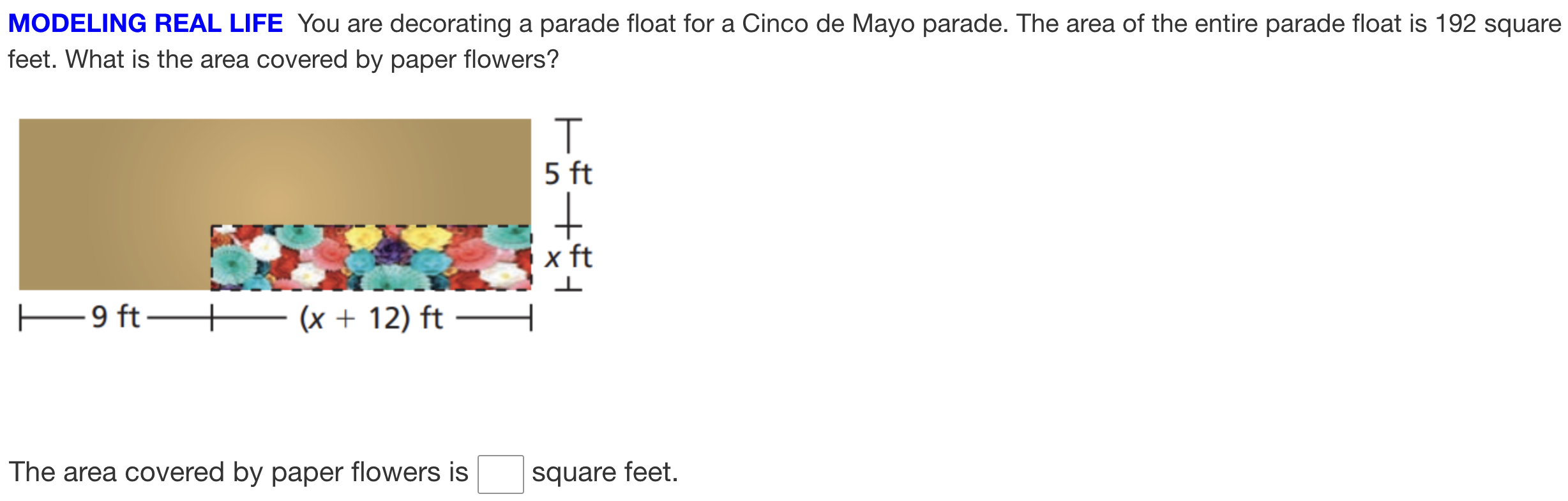
You are decorating a parade float for a Cinco de Mayo parade. The area of the entire parade float is 192 square feet. What is the area covered by paper flowers?
Understand the Problem
The question involves finding the area covered by paper flowers on a parade float. We know the total area of the float and need to determine the area of the section covered by flowers, given the float's dimensions and the flower section's dimensions in terms of 'x'. To solve this, we'll first use the total area to find the value of 'x', then use 'x' to calculate the area of the paper flower section.
Answer
$45$
Answer for screen readers
The area covered by paper flowers is $45$ square feet.
Steps to Solve
-
Find the dimensions of the entire float
The float has a width of $9 + (x + 12)$ feet and a height of $5 + x$ feet. Simplify the width: $9 + (x + 12) = x + 21$
-
Set up the equation for the area of the entire float
The area of a rectangle is width times height. The total area is given as 192 square feet.
Area = width * height
$ (x+21)(x+5) = 192 $
-
Solve for x
Expand the left side of the equation: $x^2 + 5x + 21x + 105 = 192$ $x^2 + 26x + 105 = 192$ Subtract 192 from both sides to set the equation to zero: $x^2 + 26x - 87 = 0$ Factor the quadratic equation: $(x - 3)(x + 29) = 0$ Solve for $x$: $x = 3$ or $x = -29$
-
Choose the valid solution for x
Since $x$ represents a length, it must be positive. Therefore, $x = 3$.
-
Find the dimensions of the paper flower section
The width of the paper flower section is $x + 12 = 3 + 12 = 15$ feet. The height of the paper flower section is $x = 3$ feet.
-
Calculate the area covered by paper flowers
Area of paper flowers = width * height Area = $15 * 3 = 45$ square feet.
The area covered by paper flowers is $45$ square feet.
More Information
The problem combines geometry (area calculation) with algebra (solving a quadratic equation). The solution demonstrates how to apply these mathematical concepts to a real-world scenario.
Tips
A common mistake is to forget to distribute correctly when expanding the product of the two binomials $(x+21)(x+5)$. Also, students might fail to recognize that the length cannot be negative.
AI-generated content may contain errors. Please verify critical information