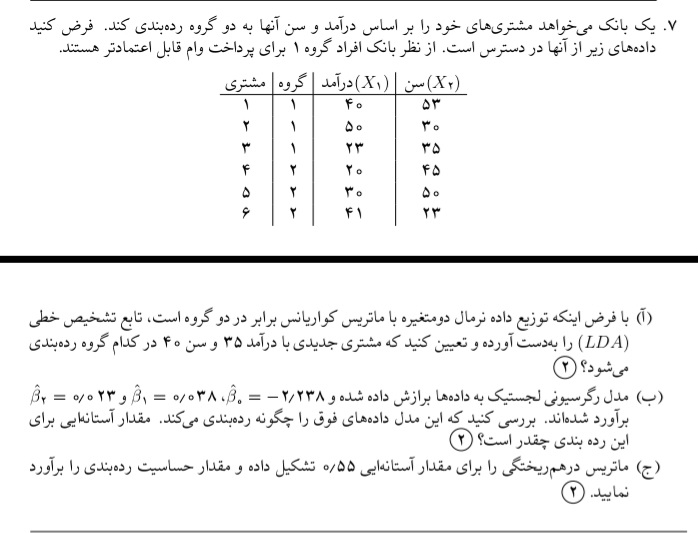
یک بانک می‌خواهد مشتری‌های خود را بر اساس درآمد و سن آنها به دو گروه دسته‌بندی کند. فرض کنید داده‌های زیر از آنها در دسترس است. از نظر بانک افراد گروه A برای پرداخت وام قابل اعتماد... یک بانک می‌خواهد مشتری‌های خود را بر اساس درآمد و سن آنها به دو گروه دسته‌بندی کند. فرض کنید داده‌های زیر از آنها در دسترس است. از نظر بانک افراد گروه A برای پرداخت وام قابل اعتماد هستند. 1) با فرض اینکه توزیع داده ها نرمال بوده و ماتریس کوواریانس برابر در دو گروه است، تابع تشخیص خطی (LDA) را بسازید و تعیین کنید که مشتری جدیدی که درآمدش ۳۵ و سنش ۴۰ سال است کدام گروه را می‌شناسد؟ 2) مدل برازش یافته به داده‌ها باید چه شکل باشد و مقدار حساسیت را ارزیابی نمایید؟ Read more

Steps to Solve

1. تعریف متغیرها و داده‌ها
   ما دو متغیر داریم: سن ($X_1$) و درآمد ($X_2$). داده‌های دو گروه باید از هم تفکیک شوند و برای هر گروه میانگین و واریانس محاسبه شود.
   داده‌های گروه 1:

• سن: 40, 50, 55, 45, 41
• درآمد: 53, 56, 55, 57, 52

داده‌های گروه 2:

• سن: 25, 28, 22, 30, 31
• درآمد: 40, 38, 42, 45, 36

2. محاسبه میانگین‌ها
   میانگین سن و درآمد هر گروه را محاسبه می‌کنیم:
   برای گروه 1:
   $$\overline{X_1^{(1)}} = \frac{40 + 50 + 55 + 45 + 41}{5} = 46.2$$
   $$\overline{X_2^{(1)}} = \frac{53 + 56 + 55 + 57 + 52}{5} = 54.6$$

برای گروه 2:
$$\overline{X_1^{(2)}} = \frac{25 + 28 + 22 + 30 + 31}{5} = 27.2$$
$$\overline{X_2^{(2)}} = \frac{40 + 38 + 42 + 45 + 36}{5} = 40.2$$

3. محاسبه واریانس و کوواریانس
   واریانس هر ویژگی را محاسبه می‌کنیم:
   برای گروه 1:
   $$S_1^{(1)} = \frac{\sum (X_i - \overline{X}^{(1)})^2}{n-1}$$

برای گروه 2:
$$S_1^{(2)} = \frac{\sum (X_i - \overline{X}^{(2)})^2}{n-1}$$

محاسبه کوواریانس:
$$Cov(X_1, X_2) = \frac{1}{n-1} \sum (X_1 - \overline{X_1})(X_2 - \overline{X_2})$$

4. مدل LDA
   مدل LDA به ما اجازه می‌دهد تا تصمیم بگیریم که کدام گروه برای یک داده خاص مناسب است. به عبارت دیگر، ما باید پارامترهای خطی را به شکل زیر محاسبه کنیم:
   $$\beta_0 = -\frac{1}{2}(\overline{X_1^{(1)}} + \overline{X_1^{(2)}})$$
   $$\beta_1 = \frac{S_1^{(1)} - S_1^{(2)}}{Cov(X_1, X_2)}$$
   $$\beta_2 = \frac{S_2^{(1)} - S_2^{(2)}}{Cov(X_1, X_2)}$$

5. تعیین گروه برای داده جدید
   با استفاده از پارامترهای LDA، گروهی که داده‌های جدید (سن = 25 و درآمد = 40) به آن تعلق دارد را تعیین می‌کنیم.