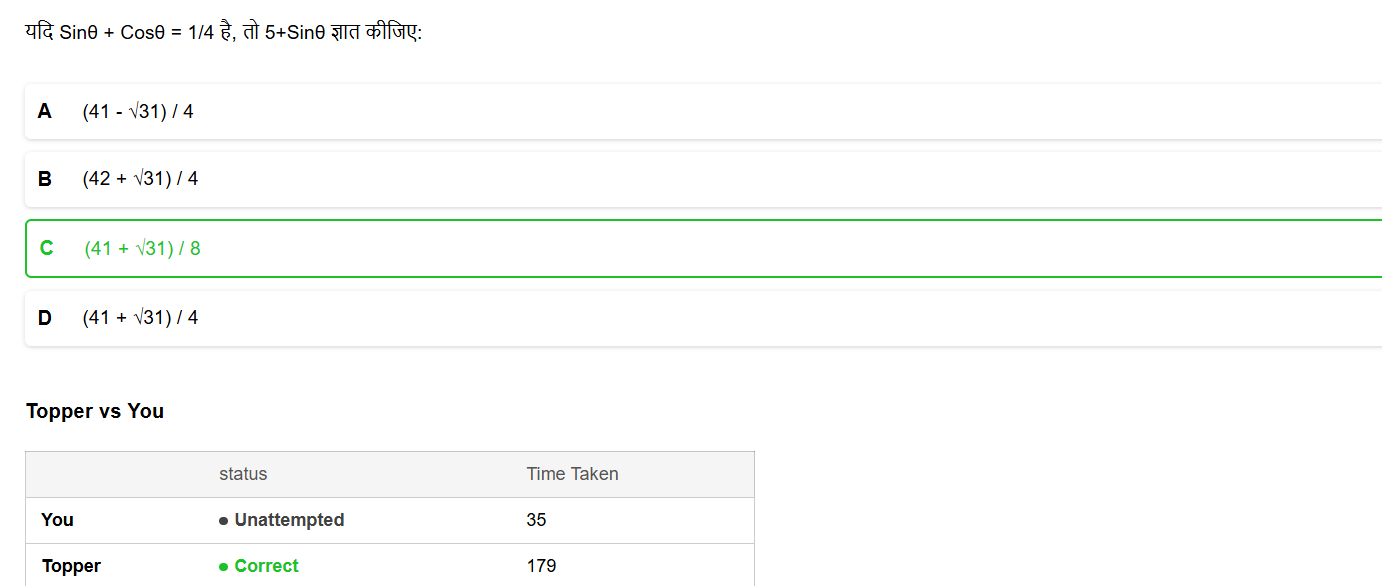
यदि sinθ + cosθ = 1/4 है, तो 5 + sinθ ज्ञात कीजिए।

Steps to Solve

1. दोनों तरफ वर्ग करें दिए गए समीकरण को दोनों तरफ से वर्ग कीजिए $\sin\theta + \cos\theta = \frac{1}{4}$: $$ (\sin\theta + \cos\theta)^2 = \left(\frac{1}{4}\right)^2 $$

2. विस्तार करें और सरल करें बाएं तरफ का विस्तार कीजिए और सर्वसमिका $sin^2\theta + cos^2\theta = 1$ का उपयोग कीजिए $$ \sin^2\theta + 2\sin\theta\cos\theta + \cos^2\theta = \frac{1}{16} $$ $$ 1 + 2\sin\theta\cos\theta = \frac{1}{16} $$

3. $2\sin\theta\cos\theta$ के लिए हल करें। $2\sin\theta\cos\theta$ के लिए हल कीजिए $$ 2\sin\theta\cos\theta = \frac{1}{16} - 1 = -\frac{15}{16} $$

4. $\sin\theta - \cos\theta$ ज्ञात कीजिए $(\sin\theta - \cos\theta )^2$ ज्ञात कीजिए $$ (\sin\theta - \cos\theta)^2 = \sin^2\theta - 2\sin\theta\cos\theta + \cos^2\theta = 1 - 2\sin\theta\cos\theta $$ उपरोक्त चरण से $2\sin\theta\cos\theta$ का मान प्रतिस्थापित कीजिए $$ (\sin\theta - \cos\theta)^2 = 1 - \left(-\frac{15}{16}\right) = 1 + \frac{15}{16} = \frac{31}{16} $$ अब, $\sin\theta - \cos\theta$ ज्ञात कीजिए $$ \sin\theta - \cos\theta = \pm\sqrt{\frac{31}{16}} = \pm\frac{\sqrt{31}}{4} $$

5. $\sin\theta$ के लिए हल करें अब हमारे पास दो समीकरण हैं: $$ \sin\theta + \cos\theta = \frac{1}{4} $$ $$ \sin\theta - \cos\theta = \pm\frac{\sqrt{31}}{4} $$ इन समीकरणों को एक साथ हल करने पर, हमें $\sin\theta$ के दो संभावित मान मिलते हैं। समीकरणों को जोड़िए: $$ 2\sin\theta = \frac{1}{4} \pm \frac{\sqrt{31}}{4} $$ $$ \sin\theta = \frac{1 \pm \sqrt{31}}{8} $$

6. $5 + \sin\theta$ ज्ञात कीजिए $5 + \sin\theta$ ज्ञात करने के लिए, $\sin\theta$ मानों में 5 जोड़िए $$ 5 + \sin\theta = 5 + \frac{1 \pm \sqrt{31}}{8} = \frac{40}{8} + \frac{1 \pm \sqrt{31}}{8} = \frac{41 \pm \sqrt{31}}{8} $$

7. सही विकल्प का पता लगाएं चूंकि केवल एक विकल्प $\frac{41 + \sqrt{31}}{8}$ है, इसलिए यह सही उत्तर है।