y = (4x^2 + 4x + 1) / (x^2 - 2x)
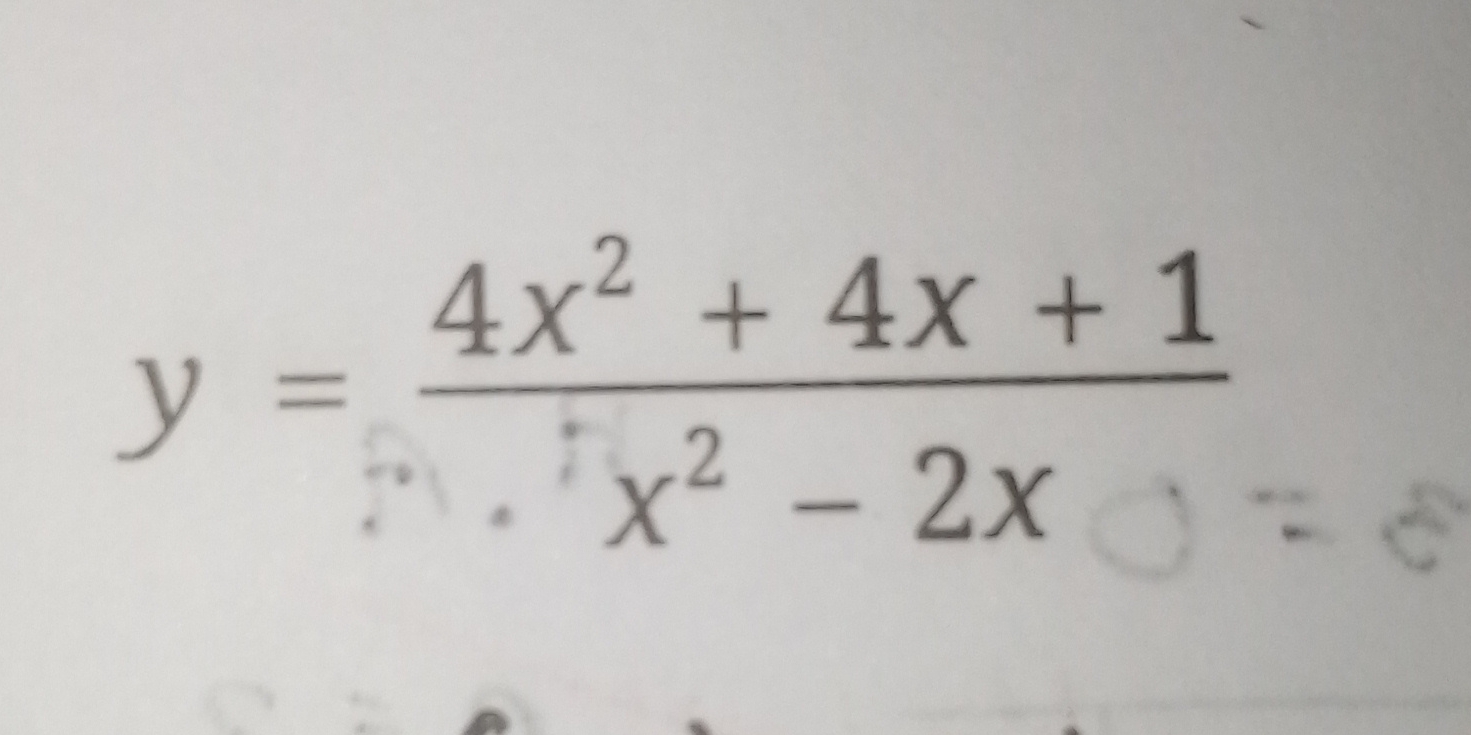
Understand the Problem
The question presents a mathematical expression involving a rational function and is likely asking for further analysis, such as simplifying, finding the domain, or maybe determining points of interest like asymptotes.
Answer
The simplified function is \( y = \frac{(2x + 1)^2}{x(x - 2)} \) with domain \( x \in \mathbb{R} \setminus \{0, 2\} \).
Answer for screen readers
The function simplified is
$$ y = \frac{(2x + 1)^2}{x(x - 2)} $$
and the domain is ( x \in \mathbb{R} \setminus {0, 2} ).
Steps to Solve
- Identify the components of the rational function
The rational function is given as:
$$ y = \frac{4x^2 + 4x + 1}{x^2 - 2x} $$
We will simplify the function, analyze the denominator, and find the domain.
- Factor the denominator
The denominator can be factored to help identify where it is undefined:
$$ x^2 - 2x = x(x - 2) $$
This shows that the function is undefined at ( x = 0 ) and ( x = 2 ).
- Factor the numerator if possible
Next, we check if the numerator can be factored. The expression is ( 4x^2 + 4x + 1 ). It can be factored as:
$$ 4x^2 + 4x + 1 = (2x + 1)^2 $$
Thus, the function can be rewritten as:
$$ y = \frac{(2x + 1)^2}{x(x - 2)} $$
- Determine the domain
The domain of the function excludes the values that make the denominator zero. Hence, the domain is:
$$ x \in \mathbb{R} \setminus {0, 2} $$
- Identify any asymptotes
Since the denominator is zero at ( x = 0 ) and ( x = 2 ), we have:
- A vertical asymptote at ( x = 0 )
- A vertical asymptote at ( x = 2 )
The function does not have horizontal asymptotes since the degree of the numerator is equal to the degree of the denominator.
The function simplified is
$$ y = \frac{(2x + 1)^2}{x(x - 2)} $$
and the domain is ( x \in \mathbb{R} \setminus {0, 2} ).
More Information
The function has vertical asymptotes at ( x = 0 ) and ( x = 2 ). It is important to understand how to factor polynomials to analyze rational functions effectively.
Tips
- Forgetting to exclude the points where the denominator equals zero from the domain.
- Not factoring the numerator properly, which could lead to incorrect conclusions about the function's behavior.
AI-generated content may contain errors. Please verify critical information