y = (4x² - 16) / (2x + 9)

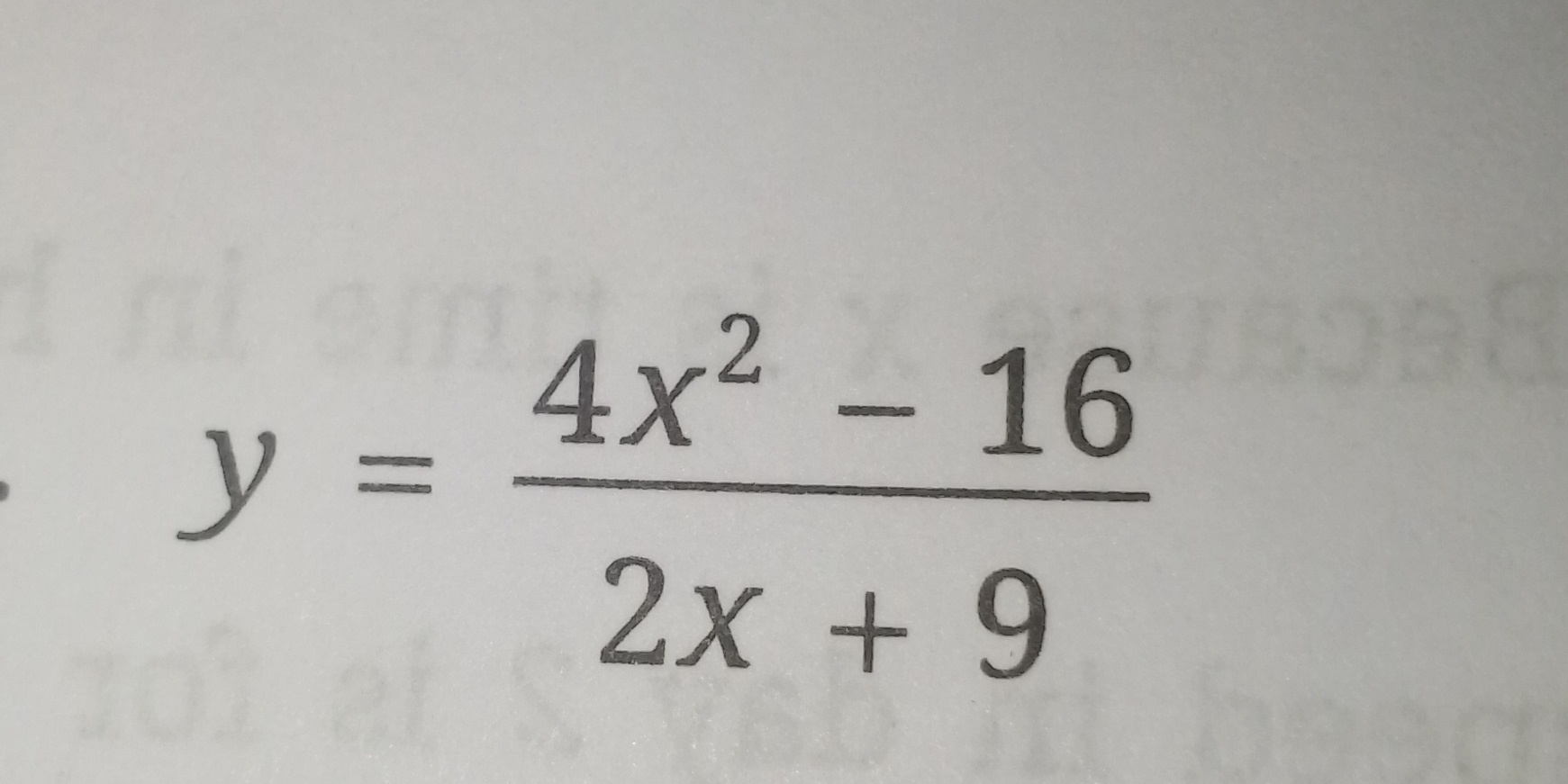
Understand the Problem

The question presents a mathematical function in the form of a rational expression. It requires analyzing or simplistically solving for the variable y based on the provided equation.

Answer

The rational function is $ y = \frac{(2x - 4)(2x + 4)}{2x + 9} $.

Steps to Solve

Identify the numerator and denominator

The function given is ( y = \frac{4x^2 - 16}{2x + 9} ). The numerator is ( 4x^2 - 16 ) and the denominator is ( 2x + 9 ).

Factor the numerator

We notice that the numerator ( 4x^2 - 16 ) can be factored as a difference of squares: $$ 4x^2 - 16 = (2x - 4)(2x + 4) $$

Rewrite the function

Substituting the factored form into the function gives: $$ y = \frac{(2x - 4)(2x + 4)}{2x + 9} $$

Simplifying the function

Since the denominator ( 2x + 9 ) cannot be factored or canceled with the numerator, the function remains: $$ y = \frac{(2x - 4)(2x + 4)}{2x + 9} $$

Finding the value of ( y )

To find specific values of ( y ), substitute various values for ( x ). For example, substituting ( x = 0 ): $$ y = \frac{4(0)^2 - 16}{2(0) + 9} = \frac{-16}{9} $$

The function is ( y = \frac{(2x - 4)(2x + 4)}{2x + 9} ).

More Information

This function can take on different values based on the input ( x ). The major feature of this function is that it is a rational expression, which means its behavior is determined by its polynomial numerator and denominator.

Tips

Forgetting to factor the numerator where applicable.
Attempting to cancel terms without ensuring they are common factors of the numerator and denominator.
Not checking the values of ( x ) that would make the denominator zero, which makes the function undefined.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!