y = 4 - x^2, y = 2 - x

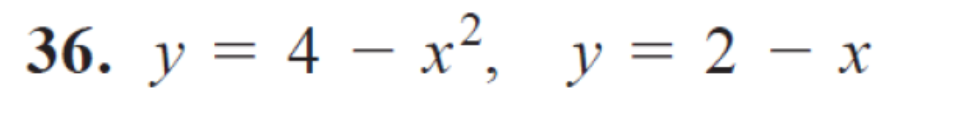
Understand the Problem

The question is asking us to solve the equations y = 4 - x² and y = 2 - x, to find the points of intersection or solutions for the system of equations.

Answer

The points of intersection are $ (2, 0) $ and $ (-1, 3) $.

Steps to Solve

Set the Equations Equal

Since both equations are equal to ( y ), we can set them equal to each other:

$$ 4 - x^2 = 2 - x $$

Rearrange the Equation

Rearranging the equation to one side gives us:

$$ x^2 - x + 2 - 4 = 0 $$

This simplifies to:

$$ x^2 - x - 2 = 0 $$

Factor the Quadratic

Next, we factor the quadratic equation:

$$ (x - 2)(x + 1) = 0 $$

Solve for ( x )

Setting each factor to zero gives us the possible ( x )-values:

$$ x - 2 = 0 \Rightarrow x = 2 $$

$$ x + 1 = 0 \Rightarrow x = -1 $$

Find Corresponding ( y )-Values

Now, we substitute each ( x ) value back into either original equation to find the corresponding ( y ) values.

For ( x = 2 ):

$$ y = 2 - 2 = 0 $$

For ( x = -1 ):

$$ y = 2 - (-1) = 3 $$

Write the Points of Intersection

The points of intersection are:

$$ (2, 0) \quad \text{and} \quad (-1, 3) $$

The points of intersection are ( (2, 0) ) and ( (-1, 3) ).

More Information

These points indicate where the curves defined by the equations intersect each other on the coordinate plane. They can represent solutions in various contexts, such as physics or economics.

Tips

Not setting equations equal: Students often forget to set the two equations equal to each other before solving.
Incorrectly factoring the quadratic: Care should be taken when factoring; double-check signs and values.
Forgetting to substitute back: Some may forget to find the corresponding ( y ) values after finding ( x )-intercepts.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!