∫ x^3 * cos(x^3) dx
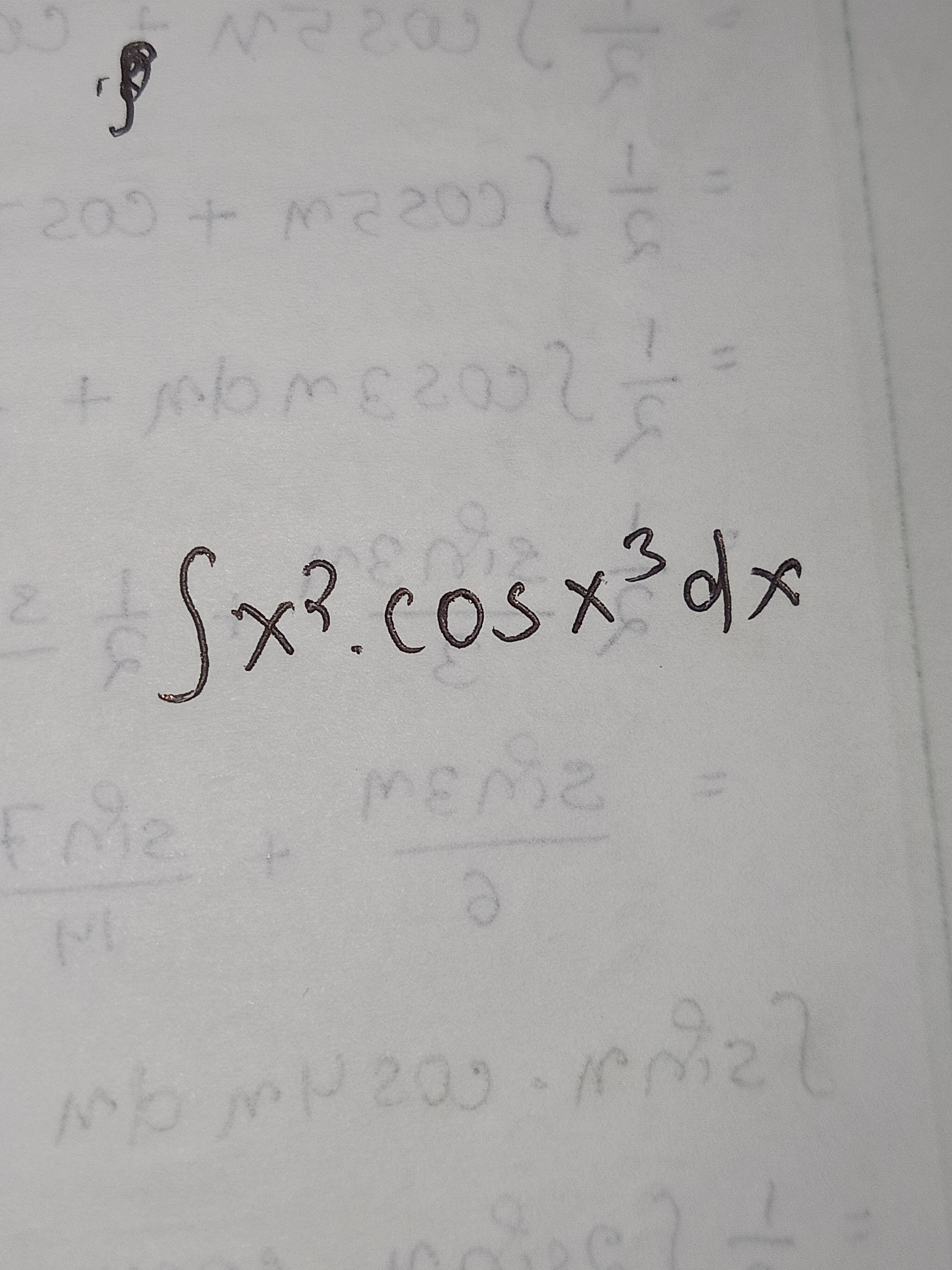
Understand the Problem
The question is asking for the integral of the expression x^3 * cos(x^3) dx. This is a calculus problem involving integration, likely solved using substitution or integration by parts.
Answer
The integral evaluates to: $$ \frac{1}{3} x^{1} \sin(x^3) - \frac{1}{9} \int \sin(x^3) x^{-\frac{2}{3}} \, dx + C $$
Answer for screen readers
The integral is given by: $$ \frac{1}{3} x^{1} \sin(x^3) - \frac{1}{9} \int \sin(x^3) x^{-\frac{2}{3}} , dx + C $$
Steps to Solve
-
Identify substitution Let ( u = x^3 ). Then, the derivative ( du = 3x^2 , dx ) implies that ( dx = \frac{du}{3x^2} ). We also need to express ( x^2 ) in terms of ( u ): ( x = u^{1/3} ) gives us ( x^2 = u^{2/3} ).
-
Rewrite the integral Substituting ( u ) into the integral, $$ \int x^3 \cos(x^3) , dx = \int u \cos(u) \cdot \frac{du}{3x^2} $$ Substituting ( x^2 ): $$ \int u \cos(u) \cdot \frac{du}{3u^{2/3}} $$ which simplifies to: $$ \frac{1}{3} \int u^{1/3} \cos(u) , du $$
-
Integration by parts Now, we use integration by parts, where we set:
- ( v = u^{1/3} ) and ( dv = \frac{1}{3} u^{-2/3} , du )
- ( dw = \cos(u) , du ) and ( w = \sin(u) )
Then, apply the integration by parts formula: $$ \int v , dw = vw - \int w , dv $$ which gives us: $$ \frac{1}{3} (u^{1/3} \sin(u) - \int \sin(u) \cdot \frac{1}{3} u^{-2/3} , du ) $$
-
Final substitution Finally, substitute back ( u = x^3 ): $$ \frac{1}{3} \left( \frac{1}{3} x^{1} \sin(x^3) - \int \sin(x^3) \cdot \frac{1}{3} (x^3)^{-2/3} , d(x^3) \right) $$ This integral is tricky but can generally be evaluated or left as part of more complex functions if necessary.
The integral is given by: $$ \frac{1}{3} x^{1} \sin(x^3) - \frac{1}{9} \int \sin(x^3) x^{-\frac{2}{3}} , dx + C $$
More Information
This integral involves a technique called integration by parts, which is useful when dealing with products of functions, especially when one is easily integrable. The result includes a residual integral which typically requires numerical methods or further techniques to evaluate.
Tips
- Forgetting to properly substitute ( dx ) based on the new variable ( u ).
- Not simplifying the integral completely before applying integration by parts.
- Confusion about which function to differentiate and which one to integrate.
