∫ x^(2/3) * √x dx
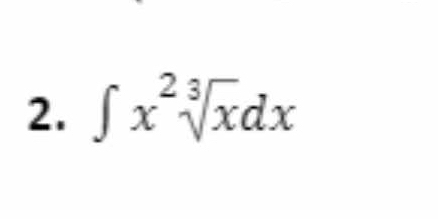
Understand the Problem
The question is asking for the evaluation of the integral of the expression x^(2/3) * sqrt(x) with respect to x. This involves using integration techniques to find the antiderivative.
Answer
The integral evaluates to $$ \frac{6}{13} x^{13/6} + C $$
Answer for screen readers
The value of the integral is $$ \frac{6}{13} x^{13/6} + C $$
Steps to Solve
-
Rewrite the integrand First, rewrite the expression inside the integral. The square root of (x) can be expressed as (x^{1/2}). Thus, we can write: $$ x^{2/3} \cdot \sqrt{x} = x^{2/3} \cdot x^{1/2} $$
-
Combine the exponents Next, use the property of exponents that states (x^a \cdot x^b = x^{a+b}): $$ x^{2/3} \cdot x^{1/2} = x^{\left(\frac{2}{3} + \frac{1}{2}\right)} $$
-
Calculate the common denominator To add the fractions (\frac{2}{3}) and (\frac{1}{2}), find a common denominator, which is 6: $$ \frac{2}{3} = \frac{4}{6} \quad \text{and} \quad \frac{1}{2} = \frac{3}{6} $$ Now add them: $$ \frac{4}{6} + \frac{3}{6} = \frac{7}{6} $$
-
Set up the integral Now that we have new exponent: $$ \int x^{7/6} , dx $$
-
Find the antiderivative To integrate ( x^{7/6} ), use the power rule for integration: $$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$ In our case, ( n = \frac{7}{6} ): $$ n + 1 = \frac{7}{6} + 1 = \frac{7}{6} + \frac{6}{6} = \frac{13}{6} $$ Thus, the integral is: $$ \int x^{7/6} , dx = \frac{x^{13/6}}{13/6} + C = \frac{6}{13} x^{13/6} + C $$
The value of the integral is $$ \frac{6}{13} x^{13/6} + C $$
More Information
This result shows the process of combining powers and using the power rule for integration. The constant (C) represents the integration constant, which is essential in indefinite integrals.
Tips
- A common mistake is forgetting to add 1 to the exponent when applying the power rule.
- Another mistake can be improper handling of fractions when adding them (like finding a common denominator).
