∫ x^(2/3) dx
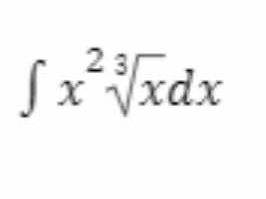
Understand the Problem
The question is asking for the evaluation of the definite integral of the function x raised to the power of 2 over the cube root of x, dx. This involves applying integration techniques to find the area under the curve represented by the function from a specified range.
Answer
The integral evaluates to \( \frac{x^{2}}{2} + C \).
Answer for screen readers
The integral evaluates to:
$$ \frac{x^{2}}{2} + C $$
Steps to Solve
- Rewrite the Integral
First, let's rewrite the integrand for clarity. The expression ( x^{2/3} \cdot x^{1/3} ) simplifies to ( x^{(2/3 + 1/3)} = x^{3/3} = x^1 ).
- Set Up the Integral
Now, we express the integral:
$$ \int x^{1} , dx $$
- Integrate the Function
To integrate ( x^1 ), we apply the power rule of integration. The power rule states that:
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
Here, ( n = 1 ), so:
$$ \int x^1 , dx = \frac{x^{1+1}}{1+1} + C = \frac{x^{2}}{2} + C $$
- Express the Final Result
Thus, the integral evaluates to:
$$ \frac{x^{2}}{2} + C $$
The integral evaluates to:
$$ \frac{x^{2}}{2} + C $$
More Information
This integral represents the antiderivative of the function ( x^1 ) or simply ( x ). The constant ( C ) represents the constant of integration, which accounts for any constant value that disappears during differentiation.
Tips
- Forgetting to combine exponents correctly when multiplying powers.
- Neglecting to include the constant of integration ( C ) in the final answer.
- Misapplying the power rule when integrating.
AI-generated content may contain errors. Please verify critical information