∫ (x² + 4) / x² dx
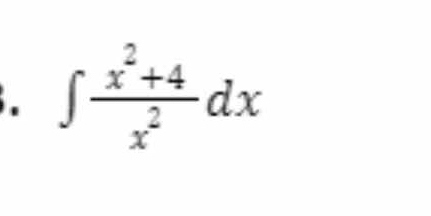
Understand the Problem
The question is asking for the integral of the function (x² + 4) / x² with respect to x. The solution will involve simplifying the expression before integrating.
Answer
$$ x - \frac{4}{x} + C $$
Answer for screen readers
The final answer is:
$$ x - \frac{4}{x} + C $$
Steps to Solve
- Simplify the Expression
Start by simplifying the integral:
$$ \frac{x^2 + 4}{x^2} = \frac{x^2}{x^2} + \frac{4}{x^2} = 1 + \frac{4}{x^2} $$
Now the integral becomes:
$$ \int \left(1 + \frac{4}{x^2}\right) dx $$
- Integrate Each Term
Now, integrate each term separately:
- The integral of 1 with respect to $x$ is $x$.
- The integral of $\frac{4}{x^2}$ can be rewritten as $4x^{-2}$, and its integral is $-4x^{-1} = -\frac{4}{x}$.
So, we have:
$$ \int \left(1 + \frac{4}{x^2}\right) dx = x - \frac{4}{x} + C $$
where $C$ is the constant of integration.
- Final Result
Therefore, the final integrated expression is:
$$ \int \frac{x^2 + 4}{x^2} dx = x - \frac{4}{x} + C $$
The final answer is:
$$ x - \frac{4}{x} + C $$
More Information
This integral combines basic integration techniques and the power rule. It simplifies the function before applying integration, making the process straightforward.
Tips
- Forgetting to include the constant of integration $C$ in the final answer.
- Failing to simplify the expression before integrating, which may lead to more complex calculations.
