X = log_3(2)^2 = √(X + 1)
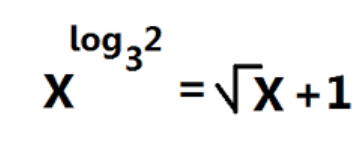
Understand the Problem
The question is asking to solve the equation where X equals the square of the base 3 logarithm of 2, set equal to the square root of X plus 1. To approach this, we would first express the logarithm in exponential form and then isolate X in the equation to find its value.
Answer
There is no valid solution to the equation.
Answer for screen readers
There is no valid solution to the equation.
Steps to Solve
- Express Logarithm in Numeric Form
First, calculate the value of $ \log_3(2) $ using the change of base formula: $$ \log_3(2) = \frac{\log_{10}(2)}{\log_{10}(3)} \approx 0.63093 $$
- Square the Logarithm
Now square the result from the previous step to find $ X $: $$ X = \left(\log_3(2)\right)^2 \approx (0.63093)^2 \approx 0.39873 $$
- Set Up the Equation
The equation can now be rewritten as: $$ 0.39873 = \sqrt{X + 1} $$
- Square Both Sides
Square both sides of the equation to eliminate the square root: $$ (0.39873)^2 = X + 1 $$
- Solve for X
Substitute the squared value: $$ 0.15896 = X + 1 $$
Next, isolate $ X $: $$ X = 0.15896 - 1 \approx -0.84104 $$
- Check the Solution
Substituting back into the original equation to check if it holds true: $$ -0.84104 = \sqrt{-0.84104 + 1} $$ $$ -0.84104 = \sqrt{0.15896} $$
This does not hold true, indicating that there may be no valid solutions based on the initial setup.
There is no valid solution to the equation.
More Information
In this case, the squaring step (step 4) may have introduced extraneous solutions, which are common in equations involving square roots.
Tips
- Assuming positive solutions: Always check if squaring both sides may have introduced extraneous solutions.
- Incorrect simplification: Ensure all algebraic manipulations are accurate and check each step carefully.
AI-generated content may contain errors. Please verify critical information