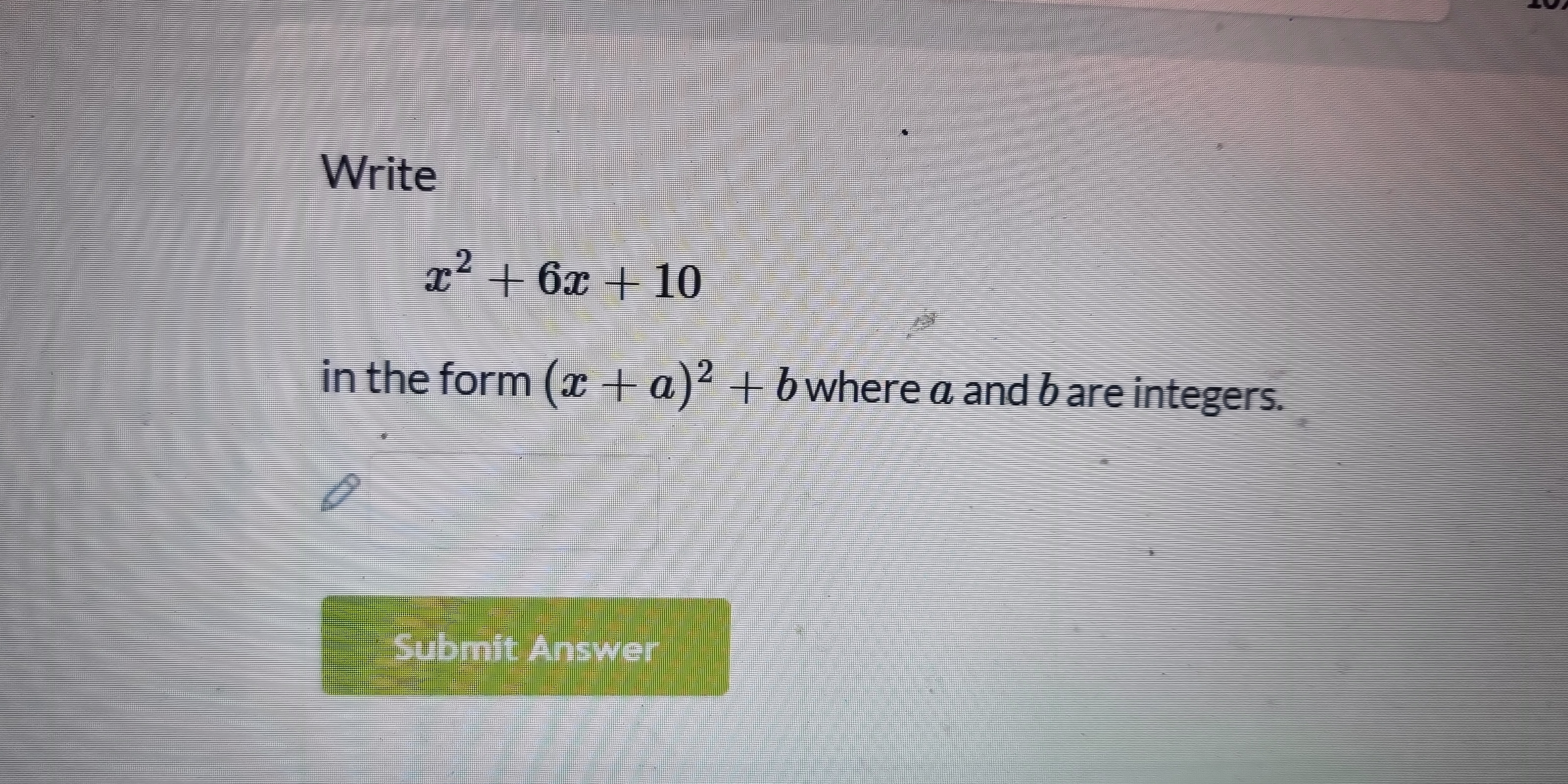
Write x² + 6x + 10 in the form (x + a)² + b where a and b are integers.
Understand the Problem
The question is asking to rewrite the quadratic expression x² + 6x + 10 in a specific form involving a perfect square and an integer. This will involve completing the square to find the values for 'a' and 'b'.
Answer
The final expression is $(x + 3)^2 + 1$ with $a = 3$ and $b = 1$.
Answer for screen readers
The expression in the desired form is: $ (x + 3)^2 + 1 $ where $a = 3$ and $b = 1$.
Steps to Solve
-
Identify the Quadratic Terms Start with the quadratic expression: $$ x^2 + 6x + 10 $$
-
Complete the Square Focus on the terms $x^2 + 6x$. To complete the square, take half of the coefficient of $x$ (which is 6), square it, and add/subtract it: $$ \left(\frac{6}{2}\right)^2 = 3^2 = 9 $$
-
Rewrite the Expression Now, add and subtract this square (9) in the original expression: $$ x^2 + 6x + 9 - 9 + 10 $$ This gives: $$ (x + 3)^2 + 1 $$
-
Final Form The expression can now be written as: $$ (x + 3)^2 + 1 $$
-
Identify Values of a and b From the final expression, we see that: $a = 3$ and $b = 1$.
The expression in the desired form is: $ (x + 3)^2 + 1 $ where $a = 3$ and $b = 1$.
More Information
Completing the square allows us to rewrite quadratic expressions in a form that makes them easier to analyze, such as finding the vertex of a parabola. The process involves adjusting the constant term to maintain an equivalent equation.
Tips
- Forgetting to Add and Subtract the Same Value: When completing the square, always add and subtract the square of half the coefficient of $x$ to maintain equality.
- Incorrectly Squaring Half of the Coefficient: Ensure you calculate half the coefficient accurately before squaring it.
AI-generated content may contain errors. Please verify critical information