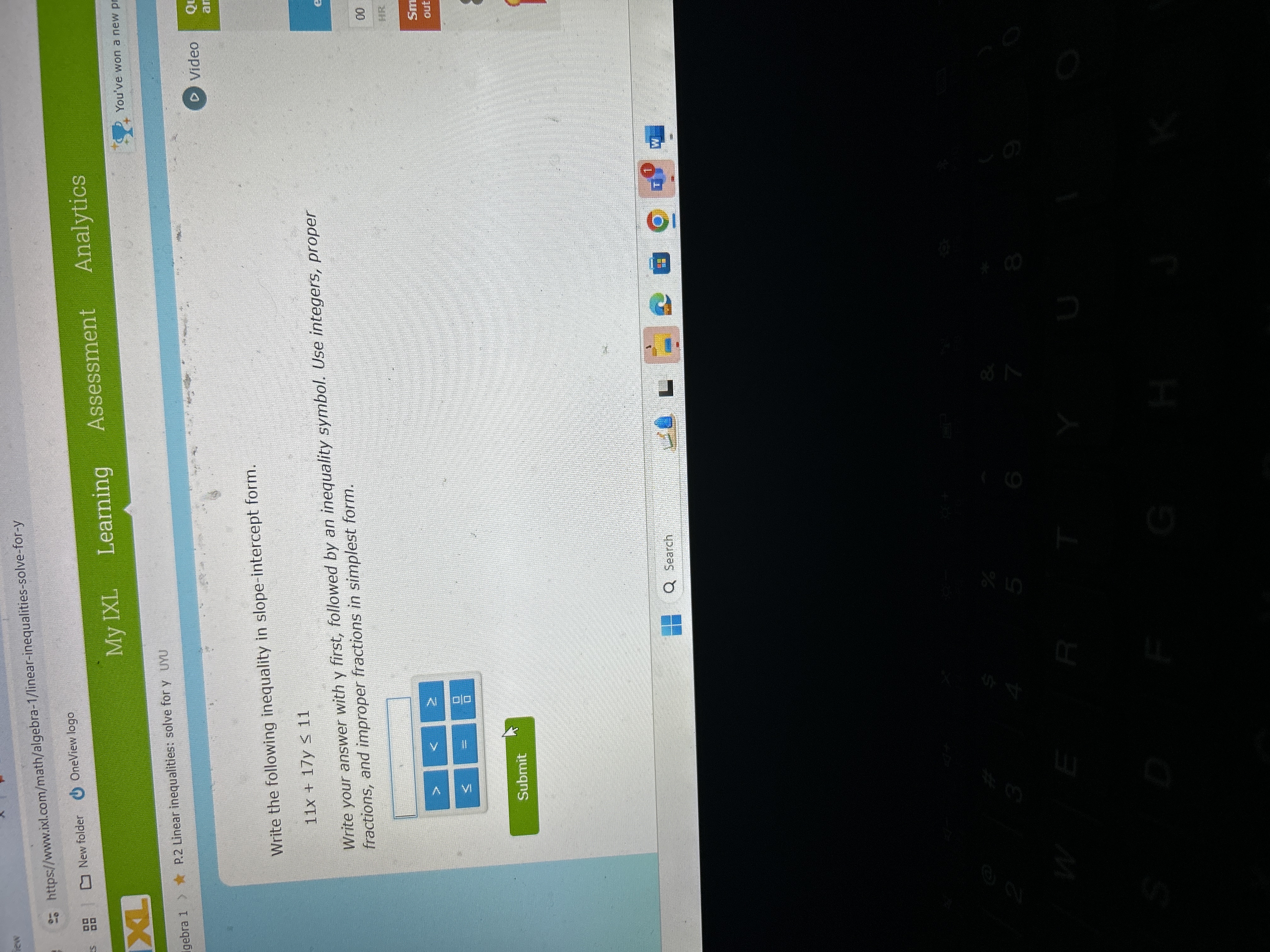
Write the following inequality in slope-intercept form. 11x + 17y ≤ 11
Understand the Problem
The question is asking to rewrite the given inequality in slope-intercept form, which is typically expressed as y = mx + b. The user needs to isolate y and express the inequality correctly.
Answer
The inequality in slope-intercept form is: $$ y \leq \frac{-11}{17}x + \frac{11}{17} $$
Answer for screen readers
The inequality in slope-intercept form is:
$$ y \leq \frac{-11}{17}x + \frac{11}{17} $$
Steps to Solve
- Isolate the y term Start by moving the term involving $x$ to the other side of the inequality. Subtract $11x$ from both sides:
$$ 17y \leq 11 - 11x $$
- Simplify the inequality Rewrite the inequality to have $y$ by itself:
$$ 17y \leq -11x + 11 $$
- Divide by the coefficient of y Now, divide all terms by 17 to solve for $y$. Remember to keep the inequality sign the same since we're dividing by a positive number:
$$ y \leq \frac{-11}{17}x + \frac{11}{17} $$
The inequality in slope-intercept form is:
$$ y \leq \frac{-11}{17}x + \frac{11}{17} $$
More Information
This inequality expresses a linear relationship where the slope is $-\frac{11}{17}$ and the y-intercept is $\frac{11}{17}$. The inequality indicates that $y$ can take values less than or equal to the expression on the right.
Tips
- Ignoring the inequality direction: Remember that dividing by a negative number would flip the inequality. However, in this case, we are dividing by a positive number, so the direction remains the same.
- Incorrectly isolating y: Ensure that all terms are correctly transferred to one side. Misplacing terms can lead to wrong coefficients in your final answer.
AI-generated content may contain errors. Please verify critical information