Write the following expression as a simplified polynomial in standard form: 2(x-5)^2 - 3(x - 5) - 7
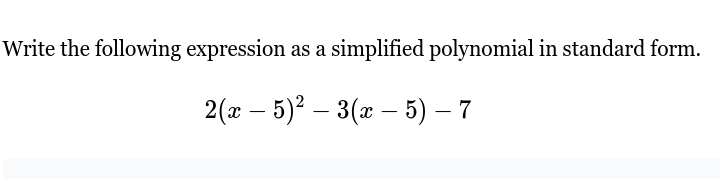
Understand the Problem
The question asks us to simplify the given polynomial expression and write it in standard form. This involves expanding the squared term, distributing the constants, combining like terms, and arranging the terms in descending order of their exponents.
Answer
$2x^{2} - 23x + 58$
Answer for screen readers
$2x^{2} - 23x + 58$
Steps to Solve
-
Expand the squared term Expand $(x-5)^2$ using the formula $(a-b)^2 = a^2 - 2ab + b^2$: $(x-5)^2 = x^2 - 2(x)(5) + 5^2 = x^2 - 10x + 25$
-
Distribute the 2 and -3 Distribute the 2 in $2(x^2 - 10x + 25)$ and the $-3$ in $-3(x - 5)$: $2(x^2 - 10x + 25) = 2x^2 - 20x + 50$ $-3(x - 5) = -3x + 15$
-
Combine the terms and simplify Combine all the terms together, including the $-7$: $2x^2 - 20x + 50 - 3x + 15 - 7$ Combine like terms: $2x^2 + (-20x - 3x) + (50 + 15 - 7)$ $2x^2 - 23x + 58$
-
Write in standard form The simplified expression is already in standard form, which means the terms are arranged in descending order of their exponents.
$2x^{2} - 23x + 58$
More Information
The standard form of a polynomial is written with the term with the highest degree first, followed by terms with decreasing degrees.
Tips
A common mistake is to forget to distribute the constants (2 and -3) correctly or make errors when combining like terms, especially with the signs. Another mistake is forgetting to expand $(x-5)^2$ correctly using the formula $(a-b)^2$. Ensure careful distribution and term combination to avoid errors.
AI-generated content may contain errors. Please verify critical information