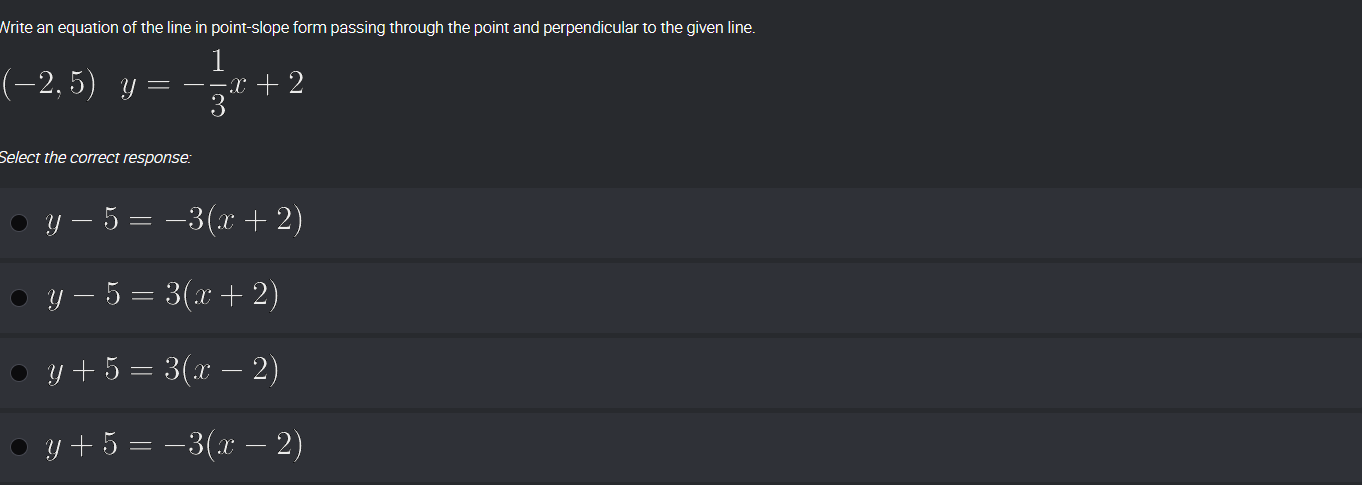
Write an equation of the line in point-slope form passing through the point (-2, 5) and perpendicular to the given line y = -1/3x + 2.
Understand the Problem
The question is asking for the equation of a line in point-slope form that passes through a specific point (-2, 5) and is perpendicular to a given line with the slope of -1/3. This requires finding the negative reciprocal of the given slope and then using the point-slope formula for the equation.
Answer
$$ y - 5 = 3(x + 2) $$
Answer for screen readers
The equation of the line in point-slope form is: $$ y - 5 = 3(x + 2) $$
Steps to Solve
-
Identify the given slope The slope of the given line is $-\frac{1}{3}$.
-
Find the perpendicular slope The slope of the line perpendicular to the given line is the negative reciprocal. Calculate it as follows: $$ \text{Perpendicular slope} = -\frac{1}{(-\frac{1}{3})} = 3 $$
-
Use the point-slope formula The point-slope form of a line is given by: $$ y - y_1 = m(x - x_1) $$ where $(x_1, y_1)$ is the point and $m$ is the slope. Here, $(x_1, y_1) = (-2, 5)$ and $m = 3$.
-
Substitute the values into the formula Substituting the point and slope into the point-slope formula: $$ y - 5 = 3(x - (-2)) $$ which simplifies to: $$ y - 5 = 3(x + 2) $$
The equation of the line in point-slope form is: $$ y - 5 = 3(x + 2) $$
More Information
This equation represents a line that passes through the point (-2, 5) and is perpendicular to the line with slope $-\frac{1}{3}$. The negative reciprocal of a slope is used to find a line perpendicular to it.
Tips
- Confusing the slope of the original line with that of the new line; always remember to take the negative reciprocal for perpendicular slopes.
- Not applying the correct point in the point-slope formula; ensure to use the provided coordinates accurately.
AI-generated content may contain errors. Please verify critical information