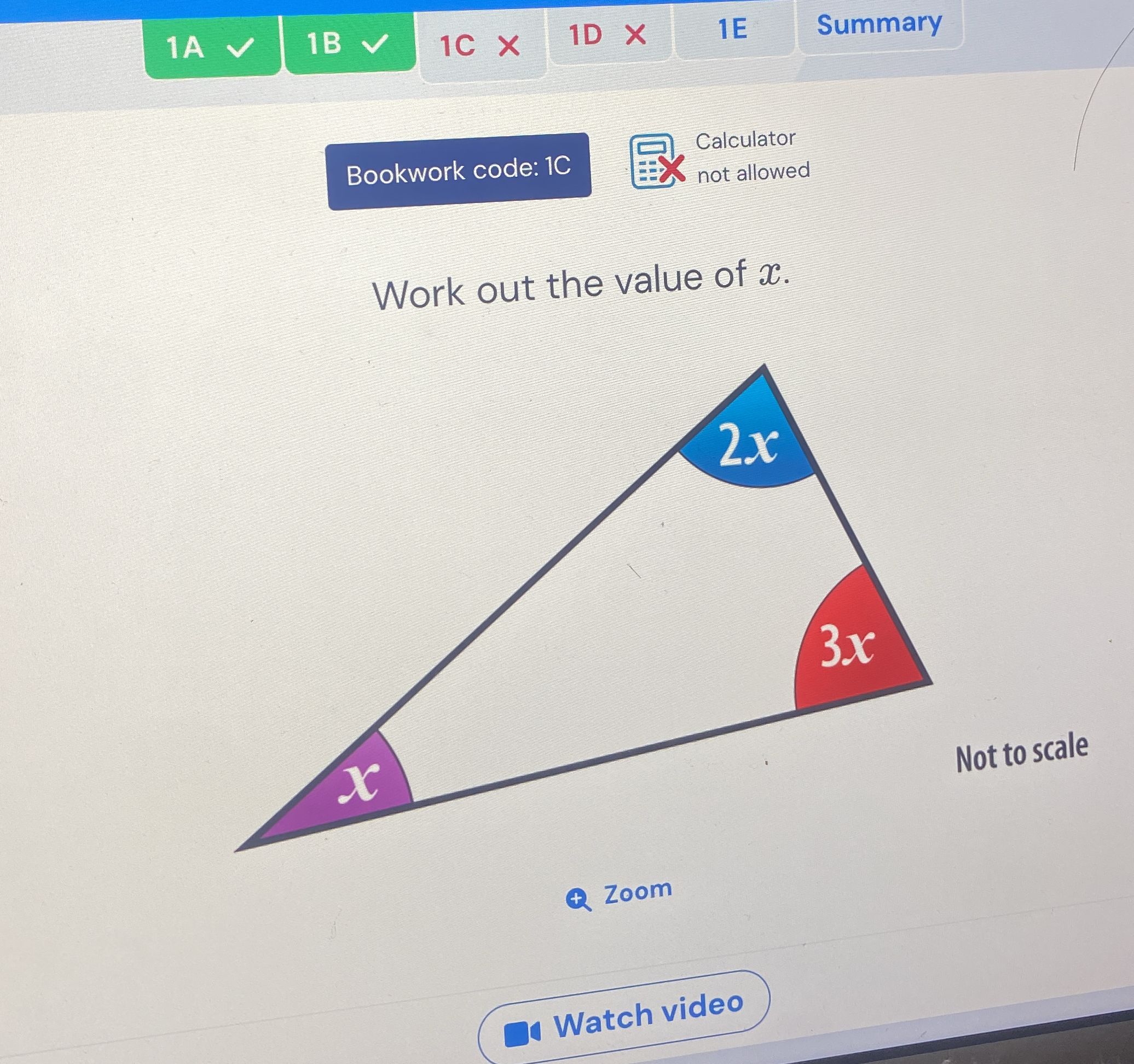
Work out the value of x.

Understand the Problem

The question is asking to determine the value of the variable x in a triangle where the angles are represented in terms of x (2x, 3x, and x). The solution will involve using the property that the sum of the angles in a triangle is equal to 180 degrees.

Answer

The value of $ x $ is $ 30 $.

Steps to Solve

Set up the equation using the triangle angle sum property

In a triangle, the sum of the angles equals ( 180^\circ ). Therefore, we can set up the equation:

$$ 2x + 3x + x = 180 $$

Combine like terms

Next, combine the ( x ) terms in the equation:

$$ 6x = 180 $$

Solve for ( x )

To isolate ( x ), divide both sides of the equation by 6:

$$ x = \frac{180}{6} $$

Calculate the value of ( x )

Now, perform the division to find the value of ( x ):

$$ x = 30 $$

The value of ( x ) is ( 30 ).

More Information

In any triangle, the sum of the interior angles is always ( 180^\circ ). This problem illustrates using algebra to find the value of a variable representing angles. The values of ( 2x ), ( 3x ), and ( x ) can also be used to find the actual measures of the angles if needed.

Tips

Forgetting the angle sum property: Some might set up the equation incorrectly by not summing all angles to equal ( 180^\circ ).
Incorrectly combining like terms: Make sure to add the coefficients of ( x ) properly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!