Work out the value of fg(6)
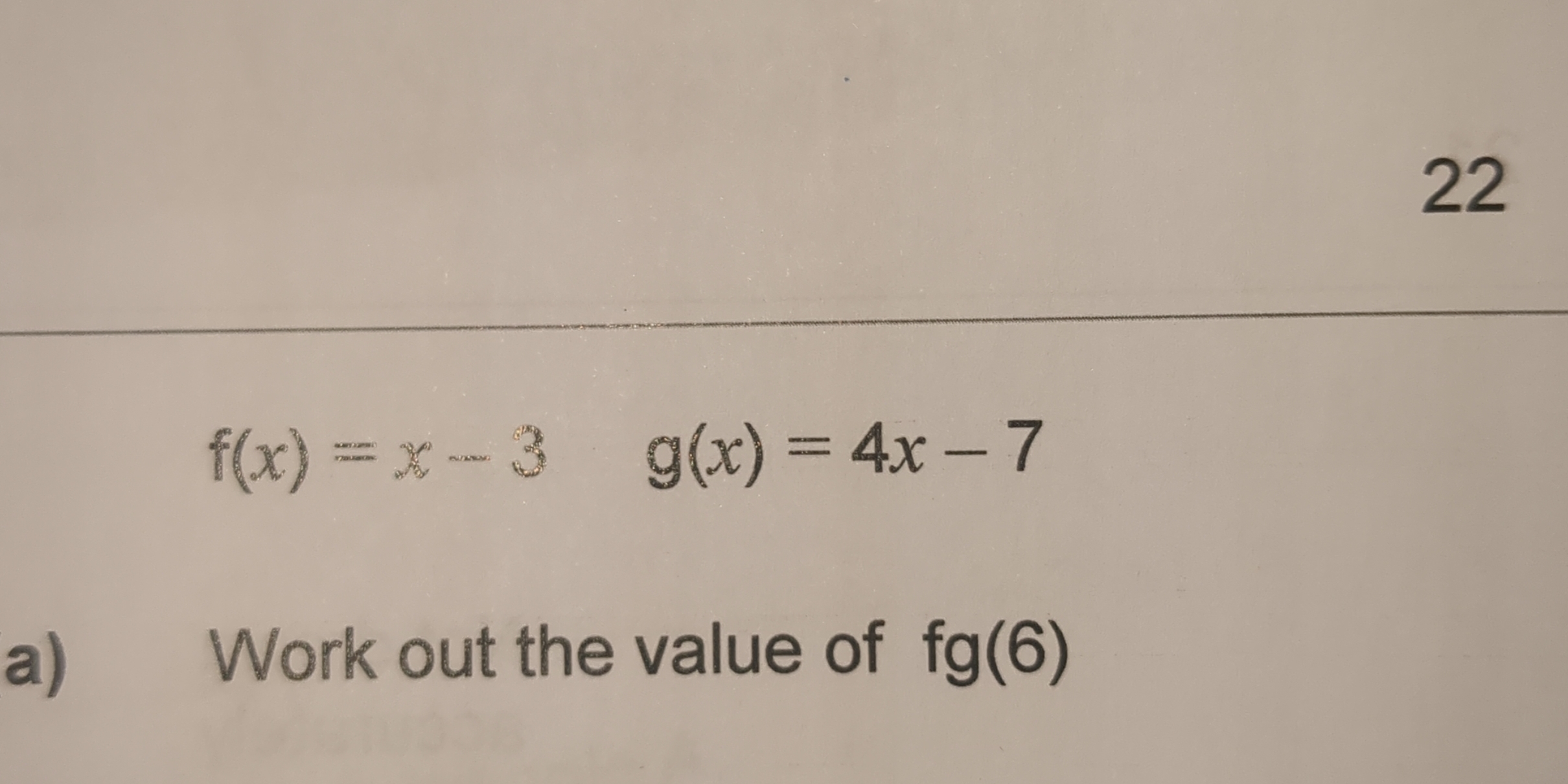
Understand the Problem
The question is asking for the value of the composite function fg evaluated at x=6, where f(x) = x - 3 and g(x) = 4x - 7. To solve this, we first need to compute g(6) and then use that result to find f(g(6)).
Answer
The value of \( fg(6) \) is \( 14 \).
Answer for screen readers
The value of ( fg(6) ) is ( 14 ).
Steps to Solve
- Calculate ( g(6) )
Substitute ( x = 6 ) into the function ( g(x) ):
$$ g(6) = 4(6) - 7 $$
Calculating this we have:
$$ g(6) = 24 - 7 = 17 $$
- Calculate ( f(g(6)) )
Now, substitute ( g(6) = 17 ) into the function ( f(x) ):
$$ f(g(6)) = f(17) = 17 - 3 $$
Calculating this we have:
$$ f(17) = 14 $$
- Final composite function result
Thus, the value of the composite function ( fg(6) ) is:
$$ fg(6) = 14 $$
The value of ( fg(6) ) is ( 14 ).
More Information
In this problem, we calculated the value of a composite function, which is a common operation in algebra. It involves first calculating the output of one function and then using that output as the input for another function.
Tips
- Confusing the order of functions: Always remember to evaluate the innermost function first, which is ( g(x) ) in this case.
- Arithmetic errors: Double-check calculations to avoid simple mistakes, especially with negative numbers.
AI-generated content may contain errors. Please verify critical information