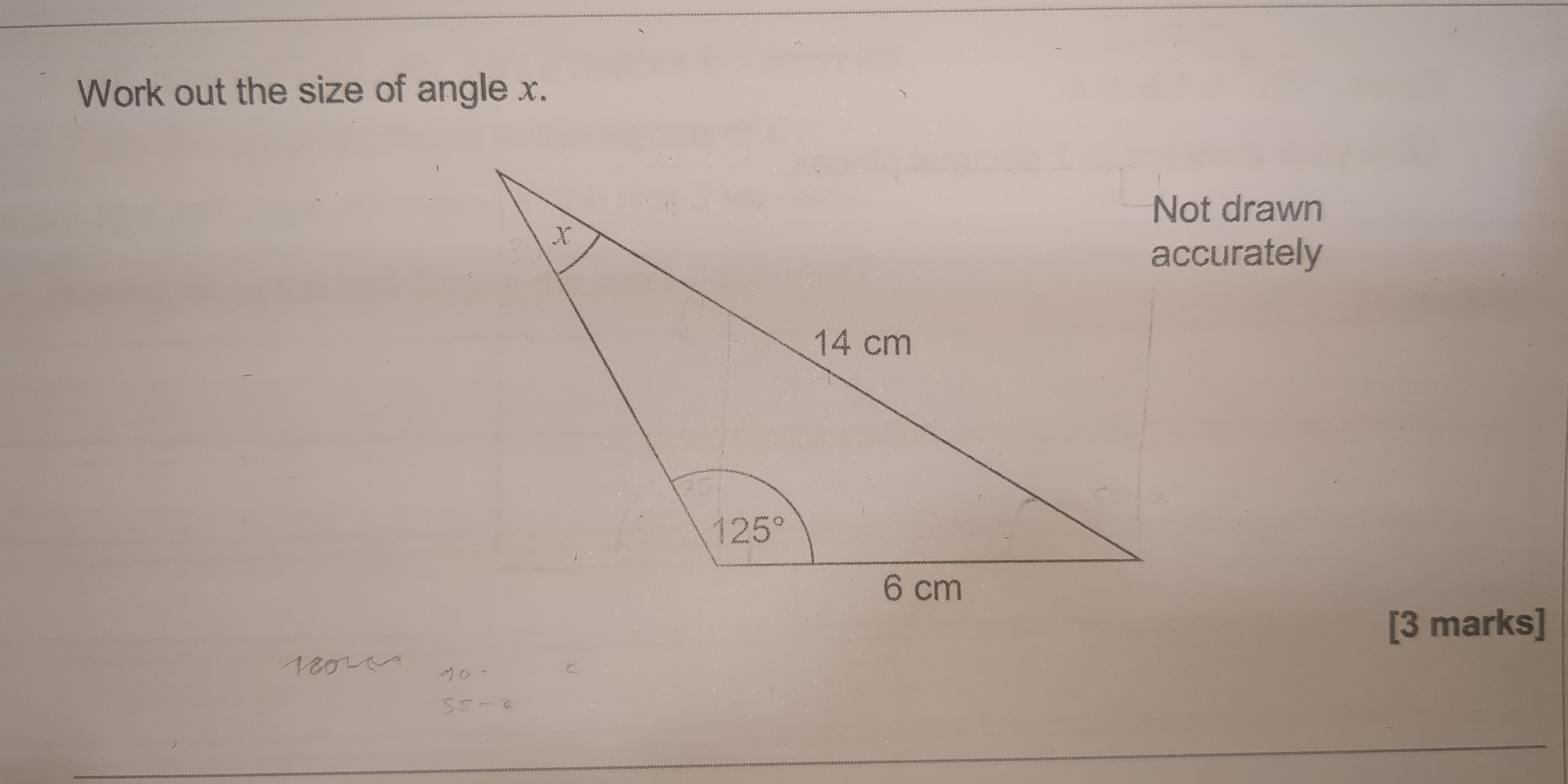
Work out the size of angle x.
Understand the Problem
The question is asking to calculate the size of angle x in a triangle, where two sides are provided along with another angle of 125°. The high-level approach to solve the problem involves using the properties of angles in a triangle, specifically the fact that the sum of angles in a triangle is always 180°.
Answer
The size of angle \( x \) is $55^\circ$.
Answer for screen readers
The size of angle ( x ) is ( 55^\circ ).
Steps to Solve
- Sum of Angles in a Triangle
The sum of all angles in a triangle equals $180^\circ$. Therefore, we can write the equation:
$$ x + 125^\circ + \text{(other angle)} = 180^\circ $$
- Calculating the Remaining Angle
Since angle ( x ) and the ( 125^\circ ) angle are the given angles, we subtract ( 125^\circ ) from ( 180^\circ ) to find the other angle in the triangle.
This gives us:
$$ \text{Other angle} = 180^\circ - 125^\circ $$
- Compute the Other Angle
Calculating the other angle yields:
$$ \text{Other angle} = 180^\circ - 125^\circ = 55^\circ $$
- Setting Up the Equation for x
Now we know that:
$$ x + 55^\circ = 180^\circ $$
- Solving for Angle x
To find ( x ), we rearrange the equation:
$$ x = 180^\circ - 55^\circ $$
- Calculate Angle x
Now, we compute ( x ):
$$ x = 180^\circ - 55^\circ = 125^\circ $$
The size of angle ( x ) is ( 55^\circ ).
More Information
In any triangle, the sum of the interior angles always equals ( 180^\circ ). This property is crucial for solving problems related to triangle angles.
Tips
- Neglecting to subtract the known angles properly. Always check your subtraction to ensure accuracy.
- Mixing up the given angles and incorrectly labeling them. Ensure you are clear about which angles are given.
AI-generated content may contain errors. Please verify critical information