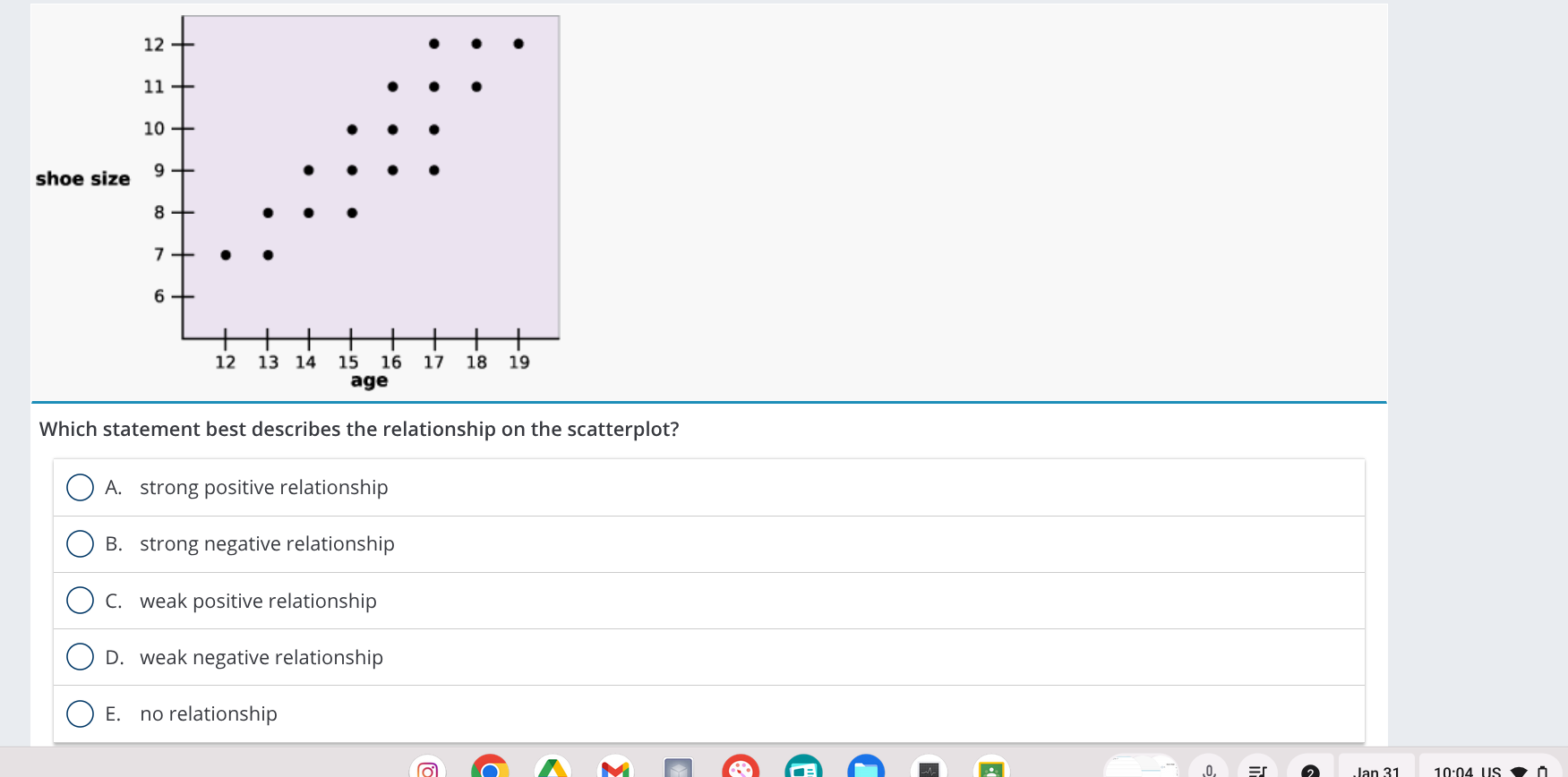
Which statement best describes the relationship on the scatterplot?
Understand the Problem
The question is asking for an analysis of a scatterplot that shows the relationship between two variables: age and shoe size. The user must evaluate the nature of this relationship based on the options provided.
Answer
The relationship is a weak positive relationship, indicating that as age increases, shoe size tends to increase slightly.
Answer for screen readers
C. weak positive relationship
Steps to Solve
-
Analyze the scatterplot
Look at the scattered points that represent the data for shoe size against age. Observe the trend in the points to determine if they are rising, falling, or showing no clear pattern. -
Assess the direction of the relationship
Determine if the relationship is positive or negative. A positive relationship means that as one variable increases (age), the other variable (shoe size) also tends to increase. Conversely, a negative relationship means that as one variable increases, the other tends to decrease. -
Evaluate the strength of the relationship
Identify how closely the points cluster around a line. A strong relationship will have points that are closely packed together along a line, whereas a weak relationship will have points that are more spread out. -
Determine the overall pattern
Based on the analysis, consolidate whether the observed relationship is strong or weak and if it's positive or negative. This will help in choosing the correct description from the options provided.
C. weak positive relationship
More Information
The scatterplot shows a general upward trend, indicating that as age increases, shoe size tends to increase as well. However, the points are somewhat spread out, suggesting that this relationship is not very strong.
Tips
- Misinterpreting the trend: Sometimes, a slight upward trend may be mistaken for a strong relationship. It’s important to note the spread of points.
- Overlooking clusters: Even if there's an upward trend, if points are widely dispersed, it's likely a weak relationship.
AI-generated content may contain errors. Please verify critical information