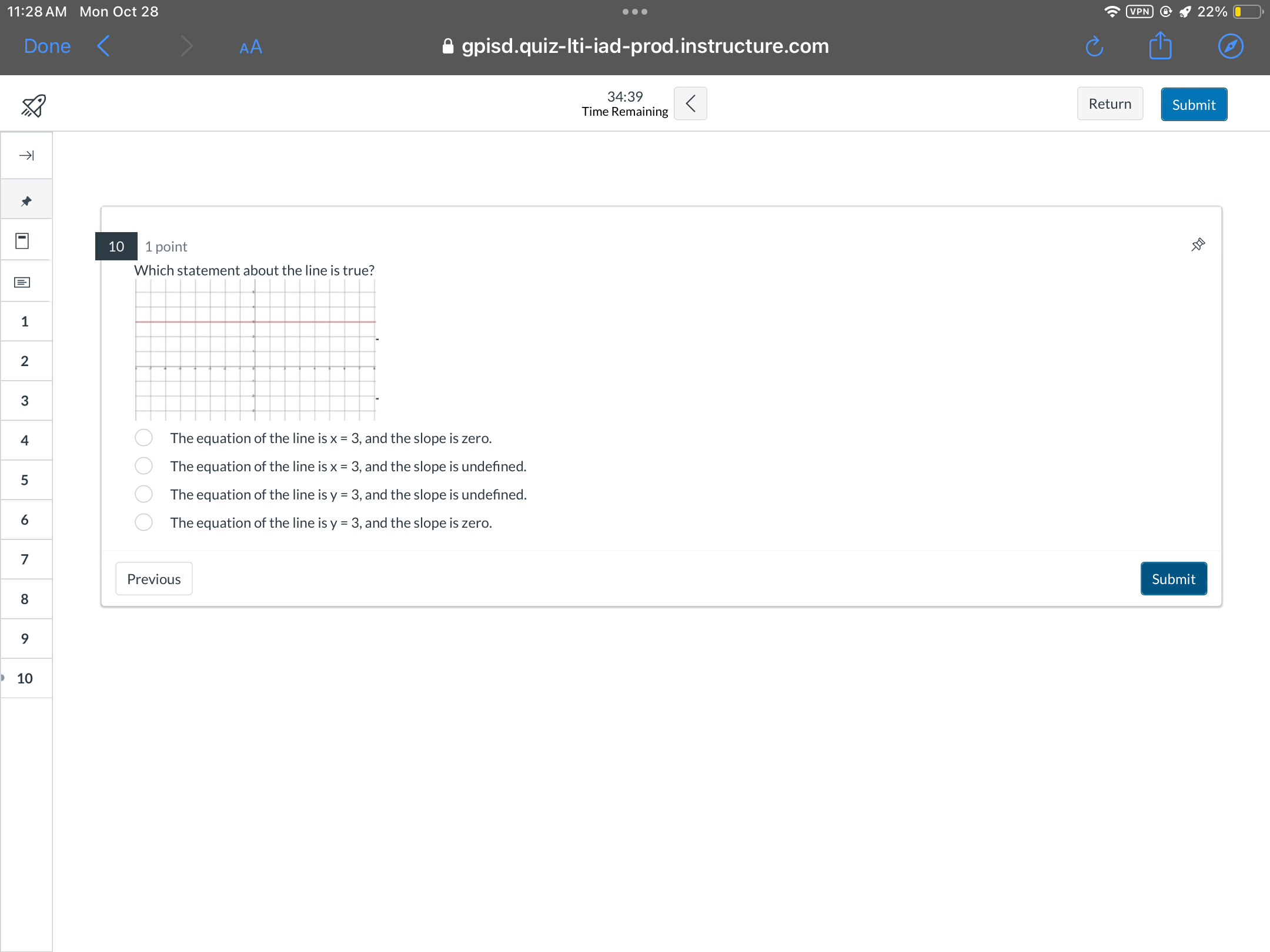
Which statement about the line is true?
Understand the Problem
The question is asking to identify the correct statement about the line depicted in a graph. It provides several options regarding the equation of the line and the nature of its slope.
Answer
The equation of the line is $y = 3$, and the slope is zero.
Answer for screen readers
The equation of the line is $y = 3$, and the slope is zero.
Steps to Solve
-
Identify the Type of Line The graph shows a horizontal line. A horizontal line has a constant $y$ value across all $x$ values.
-
Determine the Equation of the Line For a horizontal line, the equation is written in the form $y = k$, where $k$ is the constant $y$ value. From the graph, it appears that the line is at $y = 3$.
-
Calculate the Slope For a horizontal line, the slope is defined as the "rise over run." Since the line does not rise, the slope is $0$. Thus, the slope of the line is $0$.
-
Select the Correct Statement Based on the findings, the correct statement is: "The equation of the line is $y = 3$, and the slope is zero."
The equation of the line is $y = 3$, and the slope is zero.
More Information
Horizontal lines have an equation of the form $y = k$, where $k$ represents the constant value along the $y$-axis. The slope of horizontal lines is always $0$, indicating no vertical change as $x$ changes.
Tips
- Confusing horizontal lines with vertical lines. A vertical line has the equation $x = k$ and an undefined slope.
- Misinterpreting the slope as negative or positive; for horizontal lines, the slope is always $0$.
AI-generated content may contain errors. Please verify critical information