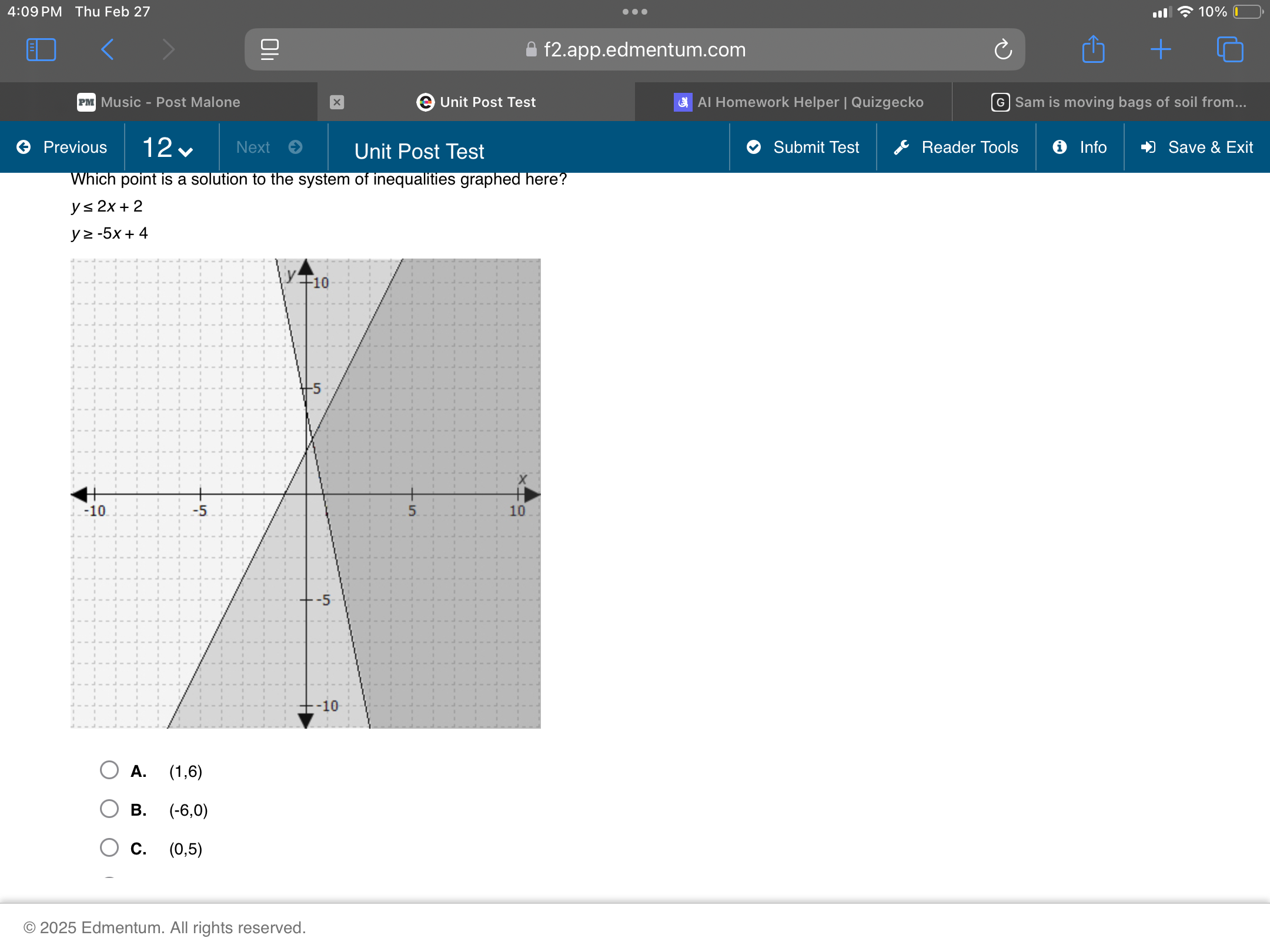
Which point is a solution to the system of inequalities graphed here? y ≤ 2x + 2 y ≥ -5x + 4

Understand the Problem

The question asks to find a point that satisfies both inequalities, (y \le 2x + 2) and (y \ge -5x + 4), which means the point must lie in the shaded region where the solutions of the two inequalities overlap. We can test each point to see if it satisfies both inequalities.

Answer

No solution among the options provided.

Steps to Solve

Test point (1, 6) in both inequalities Substitute $x = 1$ and $y = 6$ into the first inequality $y \le 2x + 2$:

$6 \le 2(1) + 2$ $6 \le 4$ This is false.

Since the point (1, 6) does not satisfy the first inequality, it cannot be a solution to the system of inequalities.

Test point (-6, 0) in both inequalities Substitute $x = -6$ and $y = 0$ into the first inequality $y \le 2x + 2$:

$0 \le 2(-6) + 2$ $0 \le -12 + 2$ $0 \le -10$ This is false.

Since the point (-6, 0) does not satisfy the first inequality, it cannot be a solution to the system of inequalities.

Test point (0, 5) in both inequalities Substitute $x = 0$ and $y = 5$ into the first inequality $y \le 2x + 2$:

$5 \le 2(0) + 2$ $5 \le 0 + 2$ $5 \le 2$ This is false.

Since the point (0, 5) does not satisfy the first inequality, it cannot be a solution to the system of inequalities.

However, there must be a mistake in the options, since none of them satisfy the two inequalities. Let's solve the inequalities as equations to find a point in the intersection area. $y = 2x + 2$ and $y = -5x + 4$.

$2x + 2 = -5x + 4$ $7x = 2$ $x = \frac{2}{7}$ $y = 2(\frac{2}{7}) + 2 = \frac{4}{7} + \frac{14}{7} = \frac{18}{7} \approx 2.57$

So the point of intersection is approximately $(\frac{2}{7}, \frac{18}{7})$, any point in the shaded area should satisfy the equation. The point (1, 6) is above the intersection. The point (-6, 0) is to the left of the intersection and below. The point (0, 5) is above the intersection on the y axis.

Given the image and the inequalities, the correct answer should be in the overlapping shaded region. However, since no answer is correct based on the current choices, there are no solutions. We will check the provided answers again to make sure we didn't make any math errors.

Re-Test Point A (1,6) $y \le 2x + 2$ $6 \le 2(1) + 2 = 4$ False

$y \ge -5x + 4$ $6 \ge -5(1) + 4 = -1$ True, so this point does not work.

Re-Test Point B (-6, 0) $y \le 2x + 2$ $0 \le 2(-6) + 2 = -10$ False

$y \ge -5x + 4$ $0 \ge -5(-6) + 4 = 34$ False, so this point does not work.

Re-Test Point C (0, 5) $y \le 2x + 2$ $5 \le 2(0) + 2 = 2$ False

$y \ge -5x + 4$ $5 \ge -5(0) + 4 = 4$ True, so this point does not work.

There is no solution among the options provided.

More Information

Since none of the points satisfied both inequalities, it means that either there was an error when creating the question, or the graph is not representative of the actual inequalities.

Tips

Incorrect substitution of x and y values into the inequalities.
Misinterpreting the inequality signs (less than or greater than).
Arithmetic errors when simplifying the inequalities after substitution.
Assuming that if a point satisfies one inequality, it automatically satisfies the other.