Which of these are solutions to the equation -6(3x + 2) = 2x - 5 - 20x - 7? Select ALL that apply.

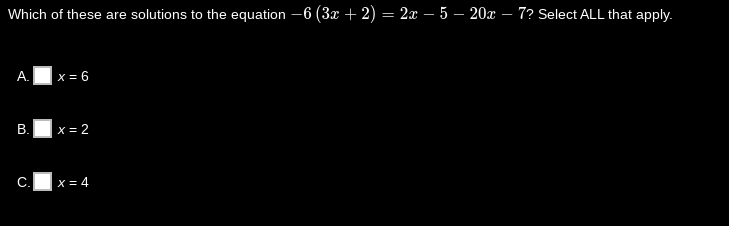
Understand the Problem

The question is asking us to determine which of the given values for 'x' satisfy the equation -6(3x + 2) = 2x - 5 - 20x - 7. We need to solve the equation to find all valid solutions and then check each option.

Answer

All of the options: $ x = 6, x = 2, x = 4 $.

Steps to Solve

Distribute on the left side of the equation

Start by distributing -6 across the terms inside the parentheses:

$$ -6(3x + 2) = -18x - 12 $$

So the equation becomes:

$$ -18x - 12 = 2x - 5 - 20x - 7 $$

Combine like terms on the right side

Combine the terms on the right side of the equation:

$$ 2x - 20x = -18x $$

and

$$ -5 - 7 = -12 $$

Therefore, the equation simplifies to:

$$ -18x - 12 = -18x - 12 $$

Analyze the resulting equation

Both sides of the equation are equal. This means the equation is true for all values of ( x ).

Check the options provided

Since the equation holds for all ( x ), we check each of the provided options (A, B, C):

( x = 6 )
( x = 2 )
( x = 4 )

All values satisfy the equation.

The solutions are ( x = 6 ), ( x = 2 ), and ( x = 4 ).

More Information

This equation simplifies to the identity ( -18x - 12 = -18x - 12 ), indicating that every value of ( x ) satisfies it. Thus, any value provided in the options will be a solution.

Tips

Ignoring combinations of terms: Failing to combine like terms properly on the right side can lead to incorrect conclusions about the equality.
Overcomplicating the analysis: Assuming the equation needs particular values when it’s valid for all real numbers could lead to confusion.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!