Which of the following statements is supported by the frequency table?

Understand the Problem

The question is asking which statement about the favorite colors of first-grade students, as represented in the frequency table, is true based on the provided data.

Answer

B: Twice as many students chose blue as chose red.

Steps to Solve

Examine the Frequency Table
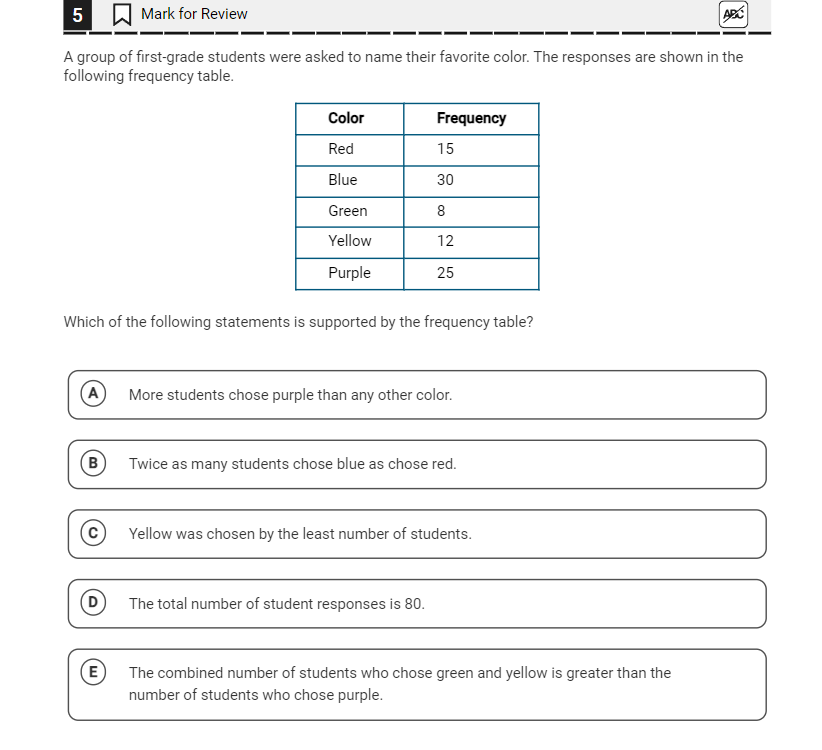
Look at the frequency table and note the number of students who chose each color:

Red: 15
Blue: 30
Green: 8
Yellow: 12
Purple: 25

Analyze Each Statement
Evaluate each statement to determine if it is true or false based on the frequency data.
Check Statement A
"More students chose purple than any other color."

Purple has 25 votes, which is less than Blue (30).
This statement is false.

Check Statement B
"Twice as many students chose blue as chose red."

Blue: 30 and Red: 15.
Checking: $30 \div 15 = 2$ (True)
This statement is true.

Check Statement C
"Yellow was chosen by the least number of students."

Yellow: 12, which is more than Green (8).
This statement is false.

Check Statement D
"The total number of student responses is 80."

Total: $15 + 30 + 8 + 12 + 25 = 90$.
This statement is false.

Check Statement E
"The combined number of students who chose green and yellow is greater than the number of students who chose purple."

Combined Green and Yellow: $8 + 12 = 20$.
Purple: 25.
This statement is false.

The statement supported by the frequency table is B: "Twice as many students chose blue as chose red."

More Information

The analysis of students' color choices reveals that Blue was chosen significantly more than Red. This allows us to confirm that the relations expressed in statement B hold true according to the data presented.

Tips

Miscalculating the total number of responses by not adding all frequencies correctly.
Misinterpreting the phrase "twice as many," leading to incorrect comparisons.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!