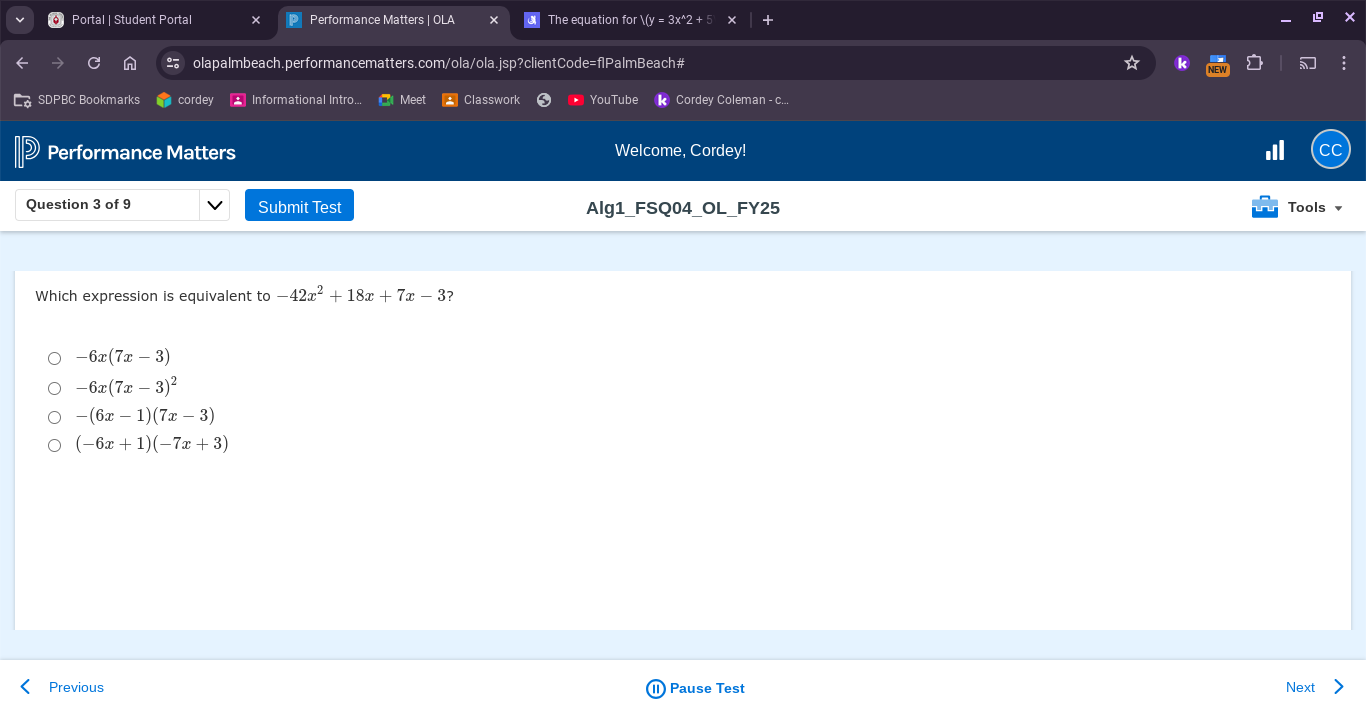
Which expression is equivalent to -42x^2 + 18x + 7x - 3?
Understand the Problem
The question asks to identify the expression that is equivalent to the given quadratic expression -42x^2 + 18x + 7x - 3. This involves factoring or expanding each of the answer choices to see which one matches the given quadratic expression.
Answer
-(6x - 1)(7x - 3)
Answer for screen readers
-(6x - 1)(7x - 3)
Steps to Solve
- Simplify the given expression
Combine like terms in the given expression: $$-42x^2 + 18x + 7x - 3 = -42x^2 + 25x - 3$$
- Evaluate the first option
Expand the first option, $-6x(7x - 3)$: $$-6x(7x - 3) = -42x^2 + 18x$$ This does not match the simplified expression.
- Evaluate the second option
Expand the second option, $-6x(7x - 3)^2$: This is $-6x(49x^2 - 42x + 9) = -294x^3 + 252x^2 - 54x$. This does not match the simplified expression.
- Evaluate the third option
Expand the third option, $-(6x - 1)(7x - 3)$: $$-(6x - 1)(7x - 3) = -(42x^2 - 18x - 7x + 3) = -(42x^2 - 25x + 3) = -42x^2 + 25x - 3$$ This matches the simplified expression.
- Evaluate the fourth option
Expand the fourth option, $(-6x + 1)(-7x + 3)$: $$(-6x + 1)(-7x + 3) = 42x^2 - 18x - 7x + 3 = 42x^2 - 25x + 3$$ This does not match the simplified expression.
-(6x - 1)(7x - 3)
More Information
The problem requires expanding algebraic expressions and comparing them to a given quadratic expression. Expanding involves using the distributive property to multiply each term in one expression by each term in another expression.
Tips
A common mistake is to incorrectly apply the distributive property or to make errors when combining like terms. Another common mistake is to forget to distribute the negative sign when expanding expressions with a leading negative sign.
AI-generated content may contain errors. Please verify critical information